题目内容
执行如图所示的程序框图,则输出的n的值是( )


| A、43 | B、44 | C、45 | D、46 |
考点:程序框图
专题:计算题,算法和程序框图
分析:算法的功能是求S=1+3+5+…+(2n-1)的值,利用等差数列的前n项公式求得S,确定满足条件条件S>2014的最小n值.
解答:
解:由程序框图知:算法的功能是求S=1+3+5+…+(2n-1)的值,
S=
×n=n2
由判断框的条件S>2014⇒n2>2014,∵442<2014,452>2014,跳出循环的n值为45.
∴输出的n值为45.
故选:C.
S=
| 1+2n-1 |
| 2 |
由判断框的条件S>2014⇒n2>2014,∵442<2014,452>2014,跳出循环的n值为45.
∴输出的n值为45.
故选:C.
点评:本题考查了循环结构的程序框图,根据框图的流程判断算法的功能是关键.

练习册系列答案
相关题目
执行如图所示的程序框图,输出的S值是( )


A、-
| ||||
B、
| ||||
| C、0 | ||||
D、
|
利用计算机在区间(0,1)上产生两个随机数a和b,则函数y=x+
-2
有零点的概率为( )
| b |
| x |
| a |
A、
| ||
B、
| ||
C、
| ||
| D、1 |
若复数z=
对应的点在直线x+2y+5=0上,则实数a的值为( )
| 1-ai |
| i |
| A、1 | B、2 | C、3 | D、4 |
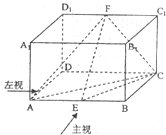 长方体ABCD-A1B1C1D1中,AA1=2,AD=3,AB=4,E,F分别在棱AB,C1D1上移动,则三棱锥F-AEC的主视图面积与左视图面积的比是( )
长方体ABCD-A1B1C1D1中,AA1=2,AD=3,AB=4,E,F分别在棱AB,C1D1上移动,则三棱锥F-AEC的主视图面积与左视图面积的比是( )