题目内容
点A(-3,3)发出的光线l射到x轴上被x轴反射,反射光线与圆C:x2+y2-4x-4y+7=0相切,则光线l所在直线方程为 .
考点:与直线关于点、直线对称的直线方程
专题:计算题,直线与圆
分析:化简圆的方程为标准方程,求出关于x轴对称的圆的方程,设l的斜率为k,利用相切求出k的值即可得到l的方程.
解答:
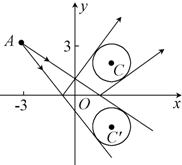 解:已知圆的标准方程是(x-2)2+(y-2)2=1,
解:已知圆的标准方程是(x-2)2+(y-2)2=1,
它关于x轴的对称圆的方程是(x-2)2+(y+2)2=1,
设光线L所在直线的方程是y-3=k(x+3)(其中斜率k待定)
由题设知对称圆的圆心C'(2,-2)到这条直线的距离等于1,
即d=
.
整理得:12k2+25k+12=0,
解得:k=-
,或k=-
.
故所求的直线方程是y-3=-
(x+3),或y-3=-
(x+3),
即3x+4y-3=0,或4x+3y+3=0.
故答案为:3x+4y-3=0,或4x+3y+3=0.
 解:已知圆的标准方程是(x-2)2+(y-2)2=1,
解:已知圆的标准方程是(x-2)2+(y-2)2=1,它关于x轴的对称圆的方程是(x-2)2+(y+2)2=1,
设光线L所在直线的方程是y-3=k(x+3)(其中斜率k待定)
由题设知对称圆的圆心C'(2,-2)到这条直线的距离等于1,
即d=
| |5k+5| | ||
|
整理得:12k2+25k+12=0,
解得:k=-
| 3 |
| 4 |
| 4 |
| 3 |
故所求的直线方程是y-3=-
| 3 |
| 4 |
| 4 |
| 3 |
即3x+4y-3=0,或4x+3y+3=0.
故答案为:3x+4y-3=0,或4x+3y+3=0.
点评:本题考查点、直线和圆的对称问题,直线与圆的关系,是基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
若变量x,y满足约束条件
,则x+2y的最大值是( )
|
| A、8 | B、0 | C、3 | D、5 |
已知单位向量
1,
的夹角为60°,则|2
-
|等于( )
| e |
| e2 |
| e1 |
| e2 |
| A、1 | ||
B、
| ||
C、
| ||
| D、2 |