题目内容
如图，在正方体ABCD-A1B1C1D1中，E为AB中点，（1）求证：AD1⊥平面CDA1B1；
（2）求异面直线C1E与AA1所成的角的正弦值．
考点：直线与平面垂直的判定,直线与平面所成的角
专题：空间位置关系与距离,空间角
分析：（1）根据题中的已知条件找到线面垂直的充分条件，然后利用线面垂直的判定进行证明．
（2）首先通过找与AA1平行的直线CC1，把异面直线问题转化为在同一平面内的直线问题，然后利用解三角形确定结果．
（2）首先通过找与AA1平行的直线CC1，把异面直线问题转化为在同一平面内的直线问题，然后利用解三角形确定结果．
解答：
证明：（1）在正方体ABCD-A1B1C1D1中，A1B1⊥平面A1ADD1，AD1?平面A1ADD1
∴A1B1⊥AD1
如图所示：AD1⊥A1D A1D∩A1B1=A1
∴：AD1⊥平面CDA1B1；
（2）设正方形的边长为2，则求得CE=
，C1E=
=3
∵A1A∥CC1
异面直线C1E与AA1所成的角就是直线C1E与CC1所成的角．
在Rt△ECC1中，
sin∠EC1C=
故答案为：（1）略
（2）sin∠EC1C=
证明：（1）在正方体ABCD-A1B1C1D1中，A1B1⊥平面A1ADD1，AD1?平面A1ADD1
∴A1B1⊥AD1
如图所示：AD1⊥A1D A1D∩A1B1=A1
∴：AD1⊥平面CDA1B1；
（2）设正方形的边长为2，则求得CE=
| 5 |
| C1C2+CE2 |
∵A1A∥CC1
异面直线C1E与AA1所成的角就是直线C1E与CC1所成的角．
在Rt△ECC1中，
sin∠EC1C=
| ||
| 3 |
故答案为：（1）略
（2）sin∠EC1C=
| ||
| 3 |
点评：本题考查的知识点：线面垂直的性质定理，线面垂直的判定定理，异面直线所成的角，勾股定理及相关的运算问题．
练习册系列答案
阅读快车系列答案
相关题目
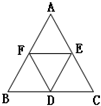
D、E、F分别是△ABC三边BC、CA、AB中点，则
+
+
=（ ）
| DE |
| EF |
| DF |
A、-
| ||||
B、-
| ||||
C、
| ||||
D、
|
经过点（-1，1），倾斜角是直线y=
x-2的倾斜角的2倍的直线方程是（ ）
| ||
| 2 |
| A、x=-1 | ||
| B、y=1 | ||
C、y-1=
| ||
D、y-1=2
|
如果两个实数之和为正数，那么这两个数（ ）
| A、一个是正数，一个是负数 |
| B、两个都是正数 |
| C、两个都是非负数 |
| D、至少有一个是正数 |