题目内容
1.已知圆O:x2+y2=4和圆C:x2+(y-4)2=1.(1)判断圆O和圆C的位置关系;
(2)过圆C的圆心C作圆O的切线l,求切线l的方程;(结果必须写成一般式).
分析 (1)求出两圆的半径和圆心距,由此能判断两圆的位置关系;
(2)设切线l的方程为:y=kx+4,由圆心O到直线l的距离等于半径,能求出切线l的方程.
解答 解:(1)因为圆O的圆心O(0,0),半径r1=2,圆C的圆心C(0,4),半径r2=1,
所以圆O和圆C的圆心距|OC|=|4-0|>r1+r2=3,
所以圆O与圆C相离.…(3分)
(2)设切线l的方程为:y=kx+4,即kx-y+4=0,
所以O到l的距离d=$\frac{4}{\sqrt{{k}^{2}+1}}$=2,解得k=$±\sqrt{3}$.
所以切线l的方程为$±\sqrt{3}$x-y+4=0.
点评 本题考查两圆位置关系的判断,考查圆的切线方程的求法,解题时要认真审题,注意两点间距离公式的合理运用.

练习册系列答案
 欣语文化快乐暑假沈阳出版社系列答案
欣语文化快乐暑假沈阳出版社系列答案
相关题目
11.若函数f(x)=$\left\{{\begin{array}{l}{1-{x^2},x<0}\\{-{x^2}-x-1,x>0}\end{array}}$,则f(f(2))的值为( )
| A. | 50 | B. | -7 | C. | -48 | D. | -49 |
9.点M(x,y)在函数y=-$\sqrt{1-{x}^{2}}$的图象上,则$\frac{y-1}{x}$的取值范围是( )
| A. | [-1,1] | B. | (-1,1) | C. | (-∞,-1)∪(1,+∞) | D. | (-∞,-1]∪[1,+∞) |
6.已知x,y满足约束条件$\left\{\begin{array}{l}2x+y-2≥0\\ x-2y+4≥0\\ 3x-y-3≤0\end{array}\right.$,目标函数z=x2+y2的最大值为( )
| A. | $\frac{{2\sqrt{5}}}{5}$ | B. | $\frac{4}{5}$ | C. | $\sqrt{13}$ | D. | 13 |
10.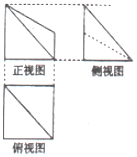 已知某几何体的三视图如图所示,俯视图中正方形的边长为2,正视图中直角梯形的两底长为1和2,则此几何体的体积为( )
已知某几何体的三视图如图所示,俯视图中正方形的边长为2,正视图中直角梯形的两底长为1和2,则此几何体的体积为( )
 已知某几何体的三视图如图所示,俯视图中正方形的边长为2,正视图中直角梯形的两底长为1和2,则此几何体的体积为( )
已知某几何体的三视图如图所示,俯视图中正方形的边长为2,正视图中直角梯形的两底长为1和2,则此几何体的体积为( )| A. | 3 | B. | $\frac{10}{3}$ | C. | $\frac{11}{3}$ | D. | 4 |
11.点(2,0,3)位于( )
| A. | Y轴上 | B. | X轴上 | C. | XOZ平面内 | D. | YOZ平面内 |

 如图,△ABC是圆O的内接三角形,P是BA的延长线上一点,且PC切圆O于点C.
如图,△ABC是圆O的内接三角形,P是BA的延长线上一点,且PC切圆O于点C.