题目内容
10．
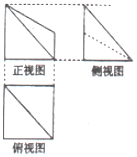已知某几何体的三视图如图所示，俯视图中正方形的边长为2，正视图中直角梯形的两底长为1和2，则此几何体的体积为（ ）| A． | 3 | B． | $\frac{10}{3}$ | C． | $\frac{11}{3}$ | D． | 4 |
分析 由已知中几何体的三视图．画出几何体的直观图，进而根据棱锥体积公式，可得答案．
解答 
解：由已知中几何体的三视图，可得几何体的直观图如下所示：
该几何体由四棱锥P-ABCD和三棱锥P-BCE组成，
四棱锥P-ABCD的体积为：$\frac{1}{3}×2×2×2$=$\frac{8}{3}$，
三棱锥P-BCE的体积为：$\frac{1}{3}×\frac{1}{2}×1×2×2$=$\frac{2}{3}$，
故该几何体的体积为$\frac{8}{3}+\frac{2}{3}$=$\frac{10}{3}$
故选B．
点评 本题考查的知识点是由三视图求体积，其中根据三视图判断几何体的形状及相关棱长的长度是解答的关键．
练习册系列答案
相关题目
20．已知点 A（1，3），B（3，1），C（-1，0），则△ABC的面积为（ ）
| A． | 5 | B． | $5\sqrt{2}$ | C． | 10 | D． | $10\sqrt{2}$ |
18．若$α∈（\frac{π}{2}，π）$，则$\frac{3}{2}cos2α=sin（\frac{π}{4}-α）$，则sin2α的值为（ ）
| A． | $\frac{2}{9}$ | B． | $-\frac{2}{9}$ | C． | $\frac{7}{9}$ | D． | $-\frac{7}{9}$ |
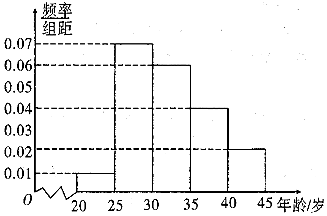“一带一路”是“丝绸之路经济带”和“21世纪海上丝绸之路”的简称，某市为了了解人们对“一带一路”的认知程度，对不同年龄和不同职业的人举办了一次“一带一路”知识竞赛，满分100分（90分及以上为认知程度高），现从参赛者中抽取了x人，按年龄分成5组（第一组：[20，25），第二组：[25，30），第三组：[30，35），第四组：[35，40），第五组：[40，45]），得到如图所示的频率分布直方图，已知第一组有6人．
20．设实数m、n、x、y满足m2+n2=a，x2+y2=b，其中a、b为正的常数，则mx+ny的最大值是（ ）
| A． | $\frac{a+b}{2}$ | B． | $\sqrt{a•b}$ | C． | $\frac{2ab}{a+b}$ | D． | $\frac{\sqrt{{a}^{2}+{b}^{2}}}{2}$ |