题目内容
数列{an}满足a1=1,an(n=2,3,4…)是非零整数,其前n项和Sn,对与任意的正整数m,n都有|Sn-Sm|≤1则{an}的通项公式为 .
考点:数列的求和
专题:等差数列与等比数列
分析:由已知得-1≤an-an+1≤1,由此能求出an=(-1)n+1.
解答:
解:∵数列{an}满足a1=1,an(n=2,3,4…)是非零整数,其前n项和Sn,
∴对与任意的正整数m,n都有|Sn-Sm|≤1,则有:
∴-1≤an≤1,(n=m+1)
∴an=(-1)n+1.
故答案为:an=(-1)n+1.
∴对与任意的正整数m,n都有|Sn-Sm|≤1,则有:
∴-1≤an≤1,(n=m+1)
∴an=(-1)n+1.
故答案为:an=(-1)n+1.
点评:本题考查数列的通项公式的求法,是基础题,解题时要注意递推公式的合理运用.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
已知函数f(x)=ex-e-x-sinx,若a,b∈R,则a+b>0是f(a)+f(b)>0成立的( )
| A、充分非必要条件 |
| B、必要非充分条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |
已知
=(1,2),
=(2x-3),且
⊥
,则x=( )
| a |
| b |
| a |
| b |
| A、3 | ||
B、-
| ||
| C、0 | ||
D、
|
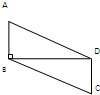 如图,在平行四边形ABCD中,2|AB|2+|BD|2-4=0,∠ABD=90°,沿BD折成直二面角A-BD-C,则空间四边形ABCD的对角线AC的长度为
如图,在平行四边形ABCD中,2|AB|2+|BD|2-4=0,∠ABD=90°,沿BD折成直二面角A-BD-C,则空间四边形ABCD的对角线AC的长度为