题目内容
过抛物线y=f(x)上一点A(1,0)的切线的倾斜角为45°则f′(1)= .
考点:利用导数研究曲线上某点切线方程,导数的运算
专题:计算题,导数的概念及应用
分析:确定点A即为切点,再根据函数的导数就是函数在此点的切线的斜率,利用斜率与倾斜角的关系,从而来求出f′(1).
解答:
解:∵点A(1,0)满足抛物线,
∴点A即为切点.
∵切线的倾斜角为45°,
∴y′=f′(1)=tan45°=1.
故答案为1.
∴点A即为切点.
∵切线的倾斜角为45°,
∴y′=f′(1)=tan45°=1.
故答案为1.
点评:本题考查函数的导数的几何意义,同时考查了直线的倾斜角和斜率的关系,属于基础题.

练习册系列答案
相关题目
根据如图图案中的圆圈排列规则,猜想第6个图形中的圆圈个数是( )
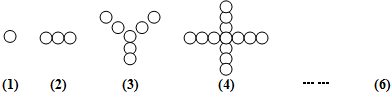

| A、20 | B、25 | C、31 | D、36 |
已知A是B的必要条件,B是C的充分条件,则A是C的( )
| A、充分条件 | B、必要条件 |
| C、充要条件 | D、无法判断 |
设f(x)=
x4-
x3+2x2+1,则( )
| 1 |
| 4 |
| 4 |
| 3 |
| A、f(x)有两个极值点0和2 |
| B、f极小=f(2) |
| C、f极大=f(0) |
| D、f(x)仅有一个极值点 |
将函数y=5sin(-3x)的周期扩大到原来的2倍,再将函数图象左移
,得到图象对应解析式是( )
| π |
| 3 |
A、y=5cos
| ||||
B、y=5sin(
| ||||
C、y=5sin(
| ||||
D、y=5sin(
|