题目内容
已知下列不等式:
(1)a2+1>2a; (2)x2+
≥1;(3)
≤2;(4)sin2x+
≥4;(5)a2+b2≥
,
其中所有正确的不等式的序号是 .
(1)a2+1>2a; (2)x2+
| 1 |
| x2+1 |
| a+b | ||
|
| 4 |
| sin2x |
| (a+b)2 |
| 2 |
其中所有正确的不等式的序号是
考点:基本不等式
专题:计算题
分析:根据函数f(x)=x2-2x+1顶点、不等式的性质不难得出结论.
解答:
解:(1)函数f(x)=x2-2x+1顶点过(1,0),取a=1时,a2+1>2a不等式不成立,故错误;
(2)令y=x2+1,原不等式可以化为y2-2y+1≥0,函数f(x)=x2-2x+1顶点过(1,0),故正确;
(3)a,b显然不能取值0,故错误.
(4)令Y=sin2x,则原不等式可化为Y2-4Y+4≥0,即(Y-2)2≥0,命题显然成立,故正确;
(5)原不等式可化为2a2+2b2≥(a+b)2
进一步化简得(a-b)2≥0,命题显然成立,故正确;
所以,答案为:(2)(4)(5)
(2)令y=x2+1,原不等式可以化为y2-2y+1≥0,函数f(x)=x2-2x+1顶点过(1,0),故正确;
(3)a,b显然不能取值0,故错误.
(4)令Y=sin2x,则原不等式可化为Y2-4Y+4≥0,即(Y-2)2≥0,命题显然成立,故正确;
(5)原不等式可化为2a2+2b2≥(a+b)2
进一步化简得(a-b)2≥0,命题显然成立,故正确;
所以,答案为:(2)(4)(5)
点评:本题考查基本不等式的性质.属于基础题.

练习册系列答案
 步步高达标卷系列答案
步步高达标卷系列答案
相关题目
根据如图图案中的圆圈排列规则,猜想第6个图形中的圆圈个数是( )
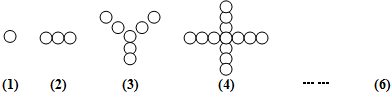

| A、20 | B、25 | C、31 | D、36 |
等比数列{an}的各项均为正数,且a5.a6=9,则log3a1+log3a2+log3a3+…+log3a10( )
| A、12 |
| B、10 |
| C、8 |
| D、2+log35 |
不等式x3-3x≥m对任意x∈[0,1]恒成立,则m的取值范围是( )
| A、(-∞,-2] |
| B、(-∞,-2) |
| C、(-∞,1) |
| D、(-∞,1] |