题目内容
已知函数f(x)=ex-e-x-sinx,若a,b∈R,则a+b>0是f(a)+f(b)>0成立的( )
| A、充分非必要条件 |
| B、必要非充分条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |
考点:必要条件、充分条件与充要条件的判断
专题:简易逻辑
分析:利用导数即可判断出函数的单调性、奇偶性,即可判断出.
解答:
解:函数f(x)=ex-e-x-sinx,∴f′(x)=ex+e-x-cosx>0,
∴函数f(x)在R上单调递增,
又f(-x)=-f(x),
∵a+b>0,∴a>-b.
∴f(a)>f(-b)=-f(b),
∴f(a)+f(b)>0.
反之也成立.
∴a+b>0是f(a)+f(b)>0成立.
故选:C.
∴函数f(x)在R上单调递增,
又f(-x)=-f(x),
∵a+b>0,∴a>-b.
∴f(a)>f(-b)=-f(b),
∴f(a)+f(b)>0.
反之也成立.
∴a+b>0是f(a)+f(b)>0成立.
故选:C.
点评:本题考查了利用导数即可判断出函数的单调性、奇偶性、简易逻辑,属于中档题.

练习册系列答案
 优秀生应用题卡口算天天练系列答案
优秀生应用题卡口算天天练系列答案 浙江之星课时优化作业系列答案
浙江之星课时优化作业系列答案 激活思维优加课堂系列答案
激活思维优加课堂系列答案
相关题目
根据如图图案中的圆圈排列规则,猜想第6个图形中的圆圈个数是( )
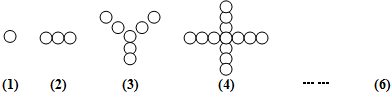

| A、20 | B、25 | C、31 | D、36 |
已知A是B的必要条件,B是C的充分条件,则A是C的( )
| A、充分条件 | B、必要条件 |
| C、充要条件 | D、无法判断 |
等比数列{an}的各项均为正数,且a5.a6=9,则log3a1+log3a2+log3a3+…+log3a10( )
| A、12 |
| B、10 |
| C、8 |
| D、2+log35 |
设f(x)=
x4-
x3+2x2+1,则( )
| 1 |
| 4 |
| 4 |
| 3 |
| A、f(x)有两个极值点0和2 |
| B、f极小=f(2) |
| C、f极大=f(0) |
| D、f(x)仅有一个极值点 |
已知a=0.50.4,b=log3
,c=log
,则a、b、c的大小关系为( )
| 3 |
| 4 |
| 1 |
| 3 |
| 1 |
| 4 |
| A、b<a<c |
| B、b<c<a |
| C、a<b<c |
| D、c<b<a |
下列推理正确的是( )
| A、把a(b+c)与loga(x+y)类比,则有:loga(x+y)=logax+logay |
| B、把a(a+b)与sin(x+y)类比,则有:sin(x+y)=sinx+siny |
| C、把(ab)n与(a+b)n类比,则有:(x+y)n=xn+yn |
| D、把(a+b)+c与(xy)z类比,则有:(xy)z=x(yz) |