题目内容
7.已知函数f(x)=x2+(sinα-2cosα)x+1是偶函数,则sinαcosα的值为( )| A. | $\frac{2}{5}$ | B. | $-\frac{2}{5}$ | C. | $±\frac{2}{5}$ | D. | 0 |
分析 利用函数的奇偶性,列出方程求解即可.
解答 解:函数f(x)=x2+(sinα-2cosα)x+1是偶函数,
可得sinα-2cosα=0,可得tanx=2.
sinαcosα=$\frac{sinαcosα}{{sin}^{2}α+{cos}^{2}α}$=$\frac{tanα}{{tan}^{2}α+1}$=$\frac{2}{5}$.
故选:A.
点评 本题考查三角函数的化简求值,函数的奇偶性的应用,考查计算能力.

练习册系列答案
 品学双优卷系列答案
品学双优卷系列答案 小学期末冲刺100分系列答案
小学期末冲刺100分系列答案 期末复习检测系列答案
期末复习检测系列答案 超能学典单元期中期末专题冲刺100分系列答案
超能学典单元期中期末专题冲刺100分系列答案
相关题目
2.a、b为非零实数,且a<b,则下列命题成立的是( )
| A. | a2<b2 | B. | $\frac{1}{{a{b^2}}}$<$\frac{1}{{{a^2}b}}$ | C. | a2b<ab2 | D. | $\frac{b}{a}$<$\frac{a}{b}$ |
12.已知定义在R上的函数y=f(x)对任意的x都满足f(x+2)=f(x),当-1≤x<1时,f(x)=x3.若函数g(x)=f(x)-loga|x|恰有6个不同零点,则a的取值范围是( )
| A. | ($\frac{1}{7}$,$\frac{1}{5}$]∪(5,7] | B. | ($\frac{1}{5}$,$\frac{1}{3}$]∪(5,7] | C. | ($\frac{1}{5}$,$\frac{1}{3}$]∪(3,5] | D. | ($\frac{1}{7}$,$\frac{1}{5}$]∪(3,5] |
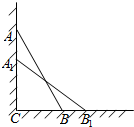 如图,一根木棒AB长为2米,斜靠在墙壁AC上,∠ABC=60°,若AB滑动至A1B1位置,且$A{A_1}=(\sqrt{3}-\sqrt{2})$米,则①BB1=$\sqrt{2}$-1米;②木棒AB的中点D所经过的路程为$\frac{π}{12}$米.
如图,一根木棒AB长为2米,斜靠在墙壁AC上,∠ABC=60°,若AB滑动至A1B1位置,且$A{A_1}=(\sqrt{3}-\sqrt{2})$米,则①BB1=$\sqrt{2}$-1米;②木棒AB的中点D所经过的路程为$\frac{π}{12}$米.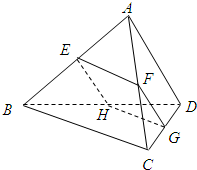 如图,空间四边形ABCD的对棱AD、BC成90°的角,且AD=BC=a,平行于AD与BC的截面分别交AB、AC、CD、BD于E、F、G、H.E在AB上,截面EGFH的最大面积是$\frac{1}{4}{a}^{2}$.
如图,空间四边形ABCD的对棱AD、BC成90°的角,且AD=BC=a,平行于AD与BC的截面分别交AB、AC、CD、BD于E、F、G、H.E在AB上,截面EGFH的最大面积是$\frac{1}{4}{a}^{2}$. 如图,四棱锥S-ABCD的底面是边长为1的正方形,SD垂直于底面ABCD,E为SC的中点,SD=AD.
如图,四棱锥S-ABCD的底面是边长为1的正方形,SD垂直于底面ABCD,E为SC的中点,SD=AD.