Question

17．如图，四棱锥S-ABCD的底面是边长为1的正方形，SD垂直于底面ABCD，E为SC的中点，SD=AD．
（1）求证：SA∥平面BDE；
（2）求直线SB与平面SAD所成角的正切值．

Answer 1

分析 （1）连结AC，交BD于O，连结OE，推导出OE∥SA，由此能证明SA∥平面BDE．
（2）由已知得AB⊥AD，AB⊥SD，从而AB⊥平面SAD，∠ASB是直线SB与平面SAD所成角，由此能求出直线SB与平面SAD所成角的正切值．

解答 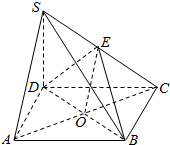证明：（1）连结AC，交BD于O，连结OE，
∵四棱锥S-ABCD的底面是边长为1的正方形，
∴O是AC的中点，
∵E为SC的中点，∴OE∥SA，
∵OE?平面BDE，SA?平面BDE，
∴SA∥平面BDE．
解：（2）∵四棱锥S-ABCD的底面是边长为1的正方形，SD垂直于底面ABCD，
∴AB⊥AD，AB⊥SD，
又SA∩SD=S，∴AB⊥平面SAD，
∴∠ASB是直线SB与平面SAD所成角，
∵SD=AD=1，∴SA=$\sqrt{1+1}=\sqrt{2}$，AB=1，AB⊥SA，
∴tan$∠ASB=\frac{AB}{SA}$=$\frac{\sqrt{2}}{2}$，
∴直线SB与平面SAD所成角的正切值为$\frac{\sqrt{2}}{2}$．

点评 本题考查线面平行的证明，考查线面角的大小的求法，是中档题，解题时要认真审题，注意空间思维能力的培养．