题目内容
19.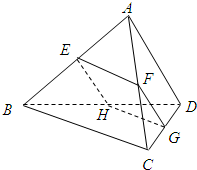 如图,空间四边形ABCD的对棱AD、BC成90°的角,且AD=BC=a,平行于AD与BC的截面分别交AB、AC、CD、BD于E、F、G、H.E在AB上,截面EGFH的最大面积是$\frac{1}{4}{a}^{2}$.
如图,空间四边形ABCD的对棱AD、BC成90°的角,且AD=BC=a,平行于AD与BC的截面分别交AB、AC、CD、BD于E、F、G、H.E在AB上,截面EGFH的最大面积是$\frac{1}{4}{a}^{2}$.
分析 由已知得∠HGF=90°,设AE:AB=x,则S四边形EFGH=EF.EH=ax•a(1-x),由此能求出当E为AB的中点时,截面的面积最大,并能求出最大面积.
解答 解:∵空间四边形ABCD的对棱AD、BC成90°的角,且AD=BC=a,
平行于AD与BC的截面分别交AB、AC、CD、BD于E、F、G、H.E在AB上,
∴∠HGF=90°,设AE:AB=x,
∵$\frac{EF}{BC}=\frac{AE}{AB}=x$,BC=a,∴EF=ax,
由$\frac{EH}{AD}=\frac{BE}{AB}=1-x$,得EH=a(1-x).
S四边形EFGH=EF.EH=ax•a(1-x)=a2•(-x2+x)
=$\frac{{a}^{2}}{4}$-a2(x-$\frac{1}{2}$)2,
当x=$\frac{1}{2}$时,${S_{最大值}}=\frac{1}{4}$a2,
即当E为AB的中点时,截面的面积最大,最大面积为${S_{最大值}}=\frac{1}{4}$a2.
故答案为:$\frac{1}{4}{a}^{2}$.
点评 本题考查截面面积的最大值的求法,是中档题,解题时要认真审题,注意配方法的合理运用.

练习册系列答案
 长江作业本同步练习册系列答案
长江作业本同步练习册系列答案
相关题目
7.已知函数f(x)=x2+(sinα-2cosα)x+1是偶函数,则sinαcosα的值为( )
| A. | $\frac{2}{5}$ | B. | $-\frac{2}{5}$ | C. | $±\frac{2}{5}$ | D. | 0 |
4.已知双曲线的一个焦点与抛物线x2=24y的焦点重合,其一条渐近线的倾斜角为60°,则该双曲线的标准方程为( )
| A. | $\frac{x^2}{9}-\frac{y^2}{27}=1$ | B. | $\frac{y^2}{9}-\frac{x^2}{27}=1$ | C. | $\frac{y^2}{27}-\frac{x^2}{9}=1$ | D. | $\frac{x^2}{27}-\frac{y^2}{9}=1$ |
8.设点O在△ABC内部且满足$\overrightarrow{OA}+\overrightarrow{OB}+\overrightarrow{OC}=\overrightarrow{0}$,现将一粒豆子撒在△ABC中,则豆子落在△OAB内的概率是( )
| A. | $\frac{1}{2}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{4}$ | D. | $\frac{2}{3}$ |