题目内容
18.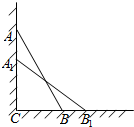 如图,一根木棒AB长为2米,斜靠在墙壁AC上,∠ABC=60°,若AB滑动至A1B1位置,且$A{A_1}=(\sqrt{3}-\sqrt{2})$米,则①BB1=$\sqrt{2}$-1米;②木棒AB的中点D所经过的路程为$\frac{π}{12}$米.
如图,一根木棒AB长为2米,斜靠在墙壁AC上,∠ABC=60°,若AB滑动至A1B1位置,且$A{A_1}=(\sqrt{3}-\sqrt{2})$米,则①BB1=$\sqrt{2}$-1米;②木棒AB的中点D所经过的路程为$\frac{π}{12}$米.
分析 根据直角三角形斜边上的中线等于斜边的一半得到CO=$\frac{1}{2}$AB=$\frac{1}{2}$A1B1=CO′,即O运动所经过的路线是一段圆弧;在Rt△ACB中,根据直角三角形三边的关系得到∠ACO=30°,CA=$\sqrt{3}$,BC=1,则易求出CA1=CA-CA1=$\sqrt{2}$,BB1=$\sqrt{2}$-1,即可得到∠A1CO′=45°,∠OCO′=15°,然后根据弧长公式计算即可.
解答  解:连接CO、CO′,如图,
解:连接CO、CO′,如图,
∵CA⊥CB,O为AB中点,O′为A1B1的中点
∴CO=$\frac{1}{2}$AB=$\frac{1}{2}$A1B1=CO′,
∵AB=2,
∴CO=1,
当A端下滑B端右滑时,AB的中点O到C的距离始终为定长1,
∴O运动所经过的路线是一段圆弧,
∵∠ABC=60°,
∴∠ACO=30°,CA=$\sqrt{3}$,BC=1
∵$A{A_1}=(\sqrt{3}-\sqrt{2})$,
CA1=CA-CA1=$\sqrt{2}$,BB1=$\sqrt{2}$-1,
∴sin∠A1B1C=$\frac{\sqrt{2}}{2}$,
∴∠A1B1C=45°,
∴∠A1CO′=45°
∴∠OCO′=15°,
∴弧OO′的长=$\frac{15π}{180}$=$\frac{π}{12}$,
即O点运动到O′所经过路线OO′的长为$\frac{π}{12}$米.
故答案为:$\sqrt{2}-1$;$\frac{π}{12}$.
点评 本题考查了动点的运动轨迹问题,解答的关键是明确AB中点在以C为圆心的圆弧上运动,考查了弧长公式及直角三角形中的边角关系,是中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
12.函数f(x)=2x-2+ex-1的零点所在区间为( )
| A. | (-1,0) | B. | (0,1) | C. | (1,2) | D. | (2,3) |
6.已知双曲线${x^2}-\frac{y^2}{b^2}=1\;(b>0)$的一个焦点是(2,0),则其渐近线的方程为( )
| A. | $\sqrt{3}x±y=0$ | B. | 3x±y=0 | C. | $x±\sqrt{3}y=0$ | D. | x±3y=0 |
7.已知函数f(x)=x2+(sinα-2cosα)x+1是偶函数,则sinαcosα的值为( )
| A. | $\frac{2}{5}$ | B. | $-\frac{2}{5}$ | C. | $±\frac{2}{5}$ | D. | 0 |
8.设点O在△ABC内部且满足$\overrightarrow{OA}+\overrightarrow{OB}+\overrightarrow{OC}=\overrightarrow{0}$,现将一粒豆子撒在△ABC中,则豆子落在△OAB内的概率是( )
| A. | $\frac{1}{2}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{4}$ | D. | $\frac{2}{3}$ |
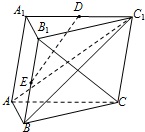 如图,在三棱柱ABC-A1B1C1中,D,E分别为A1C1,BB1的中点,B1C⊥AB,侧面BCC1B1为菱形.求证:
如图,在三棱柱ABC-A1B1C1中,D,E分别为A1C1,BB1的中点,B1C⊥AB,侧面BCC1B1为菱形.求证: