题目内容
15.已知函数f(x)=2msinx-ncosx,直线$x=\frac{π}{3}$是函数f(x)图象的一条对称轴,则$\frac{n}{m}$=-$\frac{2\sqrt{3}}{3}$.分析 由题意可得,$f(0)=f(\frac{2π}{3})$,由此能求出结果.
解答 解:∵函数f(x)=2msinx-ncosx,直线$x=\frac{π}{3}$是函数f(x)图象的一条对称轴,
∴$f(0)=f(\frac{2π}{3})$,
∴2msin0-ncos0=$2msin\frac{2π}{3}-ncos\frac{2π}{3}$,
∴-n=$\sqrt{3}m+\frac{n}{2}$,
整理,得$\frac{n}{m}$=-$\frac{2\sqrt{3}}{3}$.
故答案为:-$\frac{2\sqrt{3}}{3}$.
点评 本题主要考查函数y=Asin(ωx+φ)的图象和性质,体现了转化的数学思想,属于中档题.

练习册系列答案
相关题目
6.已知双曲线${x^2}-\frac{y^2}{b^2}=1\;(b>0)$的一个焦点是(2,0),则其渐近线的方程为( )
| A. | $\sqrt{3}x±y=0$ | B. | 3x±y=0 | C. | $x±\sqrt{3}y=0$ | D. | x±3y=0 |
7.已知函数f(x)=x2+(sinα-2cosα)x+1是偶函数,则sinαcosα的值为( )
| A. | $\frac{2}{5}$ | B. | $-\frac{2}{5}$ | C. | $±\frac{2}{5}$ | D. | 0 |
4.已知双曲线的一个焦点与抛物线x2=24y的焦点重合,其一条渐近线的倾斜角为60°,则该双曲线的标准方程为( )
| A. | $\frac{x^2}{9}-\frac{y^2}{27}=1$ | B. | $\frac{y^2}{9}-\frac{x^2}{27}=1$ | C. | $\frac{y^2}{27}-\frac{x^2}{9}=1$ | D. | $\frac{x^2}{27}-\frac{y^2}{9}=1$ |
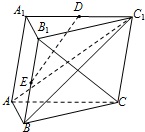 如图,在三棱柱ABC-A1B1C1中,D,E分别为A1C1,BB1的中点,B1C⊥AB,侧面BCC1B1为菱形.求证:
如图,在三棱柱ABC-A1B1C1中,D,E分别为A1C1,BB1的中点,B1C⊥AB,侧面BCC1B1为菱形.求证: