题目内容
19.已知双曲线$\frac{{x}^{2}}{4}$-$\frac{{y}^{2}}{2}$=1的焦点到渐近线的距离为a,则函数y=logax在区间[1,2]上的值域为( )| A. | [0,1] | B. | [0,2] | C. | [1,2] | D. | [1,4] |
分析 先由题中条件求出焦点坐标和渐近线方程,再代入点到直线的距离公式求出a,即可求出结论.
解答 解:由题得:其焦点坐标为(-$\sqrt{6}$,0),($\sqrt{6}$,0).渐近线方程为y=±$\frac{\sqrt{2}}{2}$x,即x±$\sqrt{2}$y=0,
∴焦点到其渐近线的距离d=$\frac{\sqrt{6}}{\sqrt{1+2}}$=$\sqrt{2}$,
∴函数y=logax在区间[1,2]上的值域为[0,2].
故选:B.
点评 本题以双曲线方程为载体,考查双曲线的标准方程,考查双曲线的几何性质,考查对数函数的性质,属于基础题.

练习册系列答案
相关题目
10.下列命题正确的是( )
| A. | 到x轴距离为5的点的轨迹是y=5 | |
| B. | 方程$\frac{x}{y}=1$表示的曲线是直角坐标平面上第一象限的角平分线 | |
| C. | 方程(x-y)2+(xy-1)2=0表示的曲线是一条直线和一条双曲线 | |
| D. | 2x2-3y2-2x+m=0通过原点的充要条件是m=0 |
9.函数y=$\frac{\sqrt{{x}^{2}+1}}{2x-1}$的导数是( )
| A. | $\frac{2+x}{\sqrt{{x}^{2}+1}(2x-1)^{2}}$ | B. | -$\frac{x+2}{\sqrt{{x}^{2}+1}(2x-1)^{2}}$ | ||
| C. | $\frac{4{x}^{2}-x+2}{(2x-1)^{2}}$ | D. | $\frac{4{x}^{2}-x+2}{(2x-1)^{2}\sqrt{{x}^{2}+1}}$ |
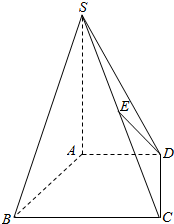 如图,在四棱锥S-ABDC中,底面ABCD是直角梯形,AB垂直于AD和BC,SA⊥底面ABCD,且SA=AB=BC=1,AD=$\frac{1}{2}$,E为SC的中点.
如图,在四棱锥S-ABDC中,底面ABCD是直角梯形,AB垂直于AD和BC,SA⊥底面ABCD,且SA=AB=BC=1,AD=$\frac{1}{2}$,E为SC的中点.