题目内容
7.已知正方体ABCD-A1B1C1D1,(1)哪些棱所在直线与直线BA1是异面直线?
(2)哪些棱所在的直线与AA1垂直?
(3)求A1B与B1D1所成角;
(4)求AC与BD1所成角.
分析 (1)根据异面直线的定义,不同在任一平面内的两直线互为异面直线,进行寻找异面直线即可;
(2)根据线面垂直的性质定理即可解题;
(3)先把异面直线转化为共面直线再做求角;
(4)连接BD交AC与点O,根据线面垂直的判定定理可知AC⊥面D1DB,而D1B?面D1DB,则AC⊥D1B,从而可求出异面直线BD1与AC所成角的余弦值.
解答 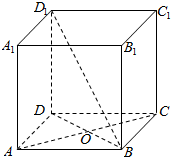 解:(1)根据异面直线的定义进行判定可知
解:(1)根据异面直线的定义进行判定可知
与直线BA1成异面直线有D1C1、D1D、C1C、C1B1、DC、AD.
(2)由题意知AA1⊥面ABCD、AA1⊥面A1B1C1D1,
∴由线面垂直点的性质定理知与AA1垂直的直线有:AB,BC,CD,DA,A1B1,B1C1,C1D1,D1A1,
(3)∵此几何体为正方体,
∴BD∥B1D1,
∴AB1与BD所成的角等于AB1与B1D1所成的角,
又∵A1D=BD,
∴AB1与BD所成的角为∠A1BD=45°
∴A1B与B1D1所成角等于45°.
(4)连接BD交AC与点O,
∵D1D⊥面ABCD,AC?面ABCD,
∴D1D⊥AC,而AC⊥BD,D1D∩BD=D,
∴AC⊥面D1DB,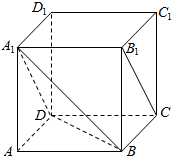
又∵D1B?面D1DB,
∴AC⊥D1B,
即直线BD1与AC所成角为90°.
点评 本题主要考查了异面直线的判定,以及异面直线及其所成的角,考查空间想象能力、运算能力和推理论证能力,属于中档题.

练习册系列答案
 学期复习一本通学习总动员期末加暑假延边人民出版社系列答案
学期复习一本通学习总动员期末加暑假延边人民出版社系列答案 芒果教辅暑假天地重庆出版社系列答案
芒果教辅暑假天地重庆出版社系列答案
相关题目
17.已知函数$f(x)=\left\{{\begin{array}{l}{2,x>m}\\{{x^2}+4x+4,x≤m}\end{array}}\right.$的图象与直线y=x恰有三个公共点,则实数m的取值范围是( )
| A. | (-∞,-1] | B. | [2,+∞) | C. | [-1,2] | D. | [-1,2) |
18.设各项均为正数的数列{an}的前n项之积为Tn,若${T_n}={2^{{n^2}+n}}$,则$\frac{{{a_n}+12}}{2^n}$的最小值为( )
| A. | 7 | B. | 8 | C. | $4\sqrt{3}$ | D. | $2\sqrt{3}$ |
15.如果a>b>0,c>d>0,则下列不等式中不正确的是( )
| A. | a-d>b-c | B. | $\frac{a}{d}$>$\frac{b}{c}$ | C. | a+d>b+c | D. | ac>bd |
12.下列各组向量中可以作为基底的是( )
| A. | $\overrightarrow{a}$=(0,0),$\overrightarrow{b}$=(1,-2) | B. | $\overrightarrow{a}$=(1,2),$\overrightarrow{b}$=(3,4) | C. | $\overrightarrow{a}$=(3,5),$\overrightarrow{b}$=(6,10) | D. | $\overrightarrow{a}$=(2,-3),$\overrightarrow{b}$=(-2,3) |
19.已知双曲线$\frac{{x}^{2}}{4}$-$\frac{{y}^{2}}{2}$=1的焦点到渐近线的距离为a,则函数y=logax在区间[1,2]上的值域为( )
| A. | [0,1] | B. | [0,2] | C. | [1,2] | D. | [1,4] |
17.在三角形ABC中,如果sin2A+sin2B=sin(A+B),且A,B都是锐角,则A+B的值为( )
| A. | $\frac{2π}{3}$ | B. | π | C. | $\frac{π}{2}$ | D. | $\frac{π}{4}$ |