题目内容
在△ABC中,角A,B,C所对的边分别为a,b,c,已知a=2
,C=45°,1+
=
,则边c的值为 .
| 3 |
| tanA |
| tanB |
| 2c |
| b |
考点:两角和与差的正切函数,同角三角函数基本关系的运用
专题:解三角形
分析:利用条件、同角三角函数的基本关系、正弦定理求得
=
,求得cosA的值,可得A的值,再利用正弦定理求得c的值.
| c |
| cosA•b |
| 2c |
| b |
解答:
解:在△ABC中,∵1+
=1+
=
=
=
=
,
故有正弦定理可得
=
,∴cosA=
,A=60°.
再由a=2
,C=45°,利用正弦定理可得
=
,即
=
,∴c=2
,
故答案为:2
.
| tanA |
| tanB |
| sinAcosB |
| cosAsinB |
| cosAsinB+sinAcosB |
| cosAsinB |
| sin(A+B) |
| cosAsinB |
| sinC |
| cosAsinB |
| 2c |
| b |
故有正弦定理可得
| c |
| cosA•b |
| 2c |
| b |
| 1 |
| 2 |
再由a=2
| 3 |
| a |
| sinA |
| c |
| sinC |
2
| ||||
|
| c | ||||
|
| 2 |
故答案为:2
| 2 |
点评:本题主要考查同角三角函数的基本关系、正弦定理的应用,属于中档题.

练习册系列答案
 习题精选系列答案
习题精选系列答案
相关题目
如图所示是一个几何体的三视图,则这个几何体外接球的表面积为( )
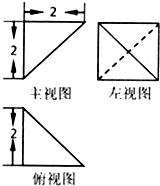

| A、8π | B、12π |
| C、16π | D、48π |
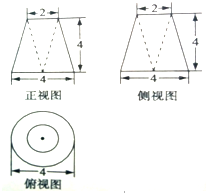
 如图,已知△ABC(|
如图,已知△ABC(|