题目内容
等比数列{an}的各项均为正数,己知a1=
,且-
,
,
成等差数列,则an= .
| 2 |
| 3 |
| 3 |
| a2 |
| 1 |
| a3 |
| 1 |
| a4 |
考点:等差数列的性质,等比数列的性质
专题:等差数列与等比数列
分析:设出等比数列的公比,结合a1=
,且-
,
,
成等差数列列式求出公比,则等比数列的通项公式可求.
| 2 |
| 3 |
| 3 |
| a2 |
| 1 |
| a3 |
| 1 |
| a4 |
解答:
解:设等比数列的公比为q(q>0),
由-
,
,
成等差数列,得:
=
-
,
又a1=
,
∴
=
-
,解得:q=
.
∴an=
×(
)n-1=2•(
)n(n∈N*).
故答案为:2•(
)n(n∈N*).
由-
| 3 |
| a2 |
| 1 |
| a3 |
| 1 |
| a4 |
| 2 |
| a3 |
| 1 |
| a4 |
| 3 |
| a2 |
又a1=
| 2 |
| 3 |
∴
| 2 | ||
|
| 1 | ||
|
| 3 | ||
|
| 1 |
| 3 |
∴an=
| 2 |
| 3 |
| 1 |
| 3 |
| 1 |
| 3 |
故答案为:2•(
| 1 |
| 3 |
点评:本题考查等比数列的通项公式,考查等差数列的性质,是基础的计算题.

练习册系列答案
相关题目
下列说法正确的是( )
| A、“a>b”是“a2>b2”的充分不必要条件 |
| B、命题“?x0∈R,x02+1<0”的否定是:“?x∈R,x2+1>0” |
| C、关于x的方程x2+(a+1)x+a-2=0的两根异号的充要条件是a<1 |
| D、若f(x)为R上的偶函数,则f(x-1)的图象关于直线x=1对称 |
函数f(x)=sin(ωx+φ)(ω>0,|φ|<
)的最小正周期为π,若其图象向右平移
个单位后得到的函数时奇函数,则函数f(x)的图象( )
| π |
| 2 |
| π |
| 6 |
A、在(0,
| ||
B、在(0,
| ||
C、关于直线x=
| ||
D、关于点(
|
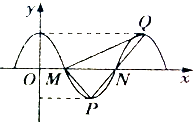 已知函数f(x)=Acosωx(ω>0)的部分图象如图所示,且∠MQP=
已知函数f(x)=Acosωx(ω>0)的部分图象如图所示,且∠MQP= 若如图框图所给程序运行的结果为S=360,那么判断框中应填入的关于k的判断条件是k<
若如图框图所给程序运行的结果为S=360,那么判断框中应填入的关于k的判断条件是k<