题目内容
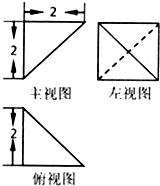
如图所示是一个几何体的三视图，则这个几何体外接球的表面积为（ ）
| A、8π | B、12π |
| C、16π | D、48π |
考点：由三视图求面积、体积
专题：计算题,空间位置关系与距离
分析：几何体是三棱锥，结合直观图判断三棱锥的结构特征，根据三视图的数据求得外接球的半径，代入球的表面积公式计算．
解答：
解：由三视图知：几何体是三棱锥，如图三棱锥S=ABC，
其中SD⊥平面ACBD，四边形ACBD为边长为2的正方形，SD=2，
∴外接球的球心为SC是中点O，
∴外接球的半径R=
=
，
∴外接球的表面积S=4π×3=12π．
故选：B．
其中SD⊥平面ACBD，四边形ACBD为边长为2的正方形，SD=2，
∴外接球的球心为SC是中点O，
∴外接球的半径R=
| ||
| 2 |
| 3 |
∴外接球的表面积S=4π×3=12π．
故选：B．
点评：本题考查了由三视图求几何体的外接球的表面积，根据三视图判断几何体的形状及数据所对应的几何量是解题的关键．
练习册系列答案
相关题目
在△ABC中，∠BAC=60°，点O满足2
+
+
=
，且OC⊥OA，则
的值为（ ）
| OA |
| OB |
| OC |
| 0 |
| AB |
| AC |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
已知全集U=R，A=|x|-2＜x＜2|，B={x|-
＜x＜
}，则（ ）
| 2 |
| 2 |
| A、A∩B=∅ |
| B、A∪B=R |
| C、A∪（∁UB）=R |
| D、A?B |
函数f（x）=sin（ωx+φ）（ω＞0，|φ|＜
）的最小正周期为π，若其图象向右平移
个单位后得到的函数时奇函数，则函数f（x）的图象（ ）
| π |
| 2 |
| π |
| 6 |
A、在（0，
| ||
B、在（0，
| ||
C、关于直线x=
| ||
D、关于点（
|
| 1-2i |
| 2+i |
| A、-i | ||
B、-
| ||
C、
| ||
D、
|
已知实数x，y满足
，则x2+y2+4x+6y+14的最大值为（ ）
|
| A、42 | ||
B、
| ||
C、
| ||
| D、46 |
设非零向量
，
，
，满足|
|=|
|=|
|，
+
=
，
与
的夹角为（ ）
| a |
| b |
| c |
| a |
| b |
| c |
| a |
| b |
| c |
| b |
| c |
| A、60° | B、90° |
| C、120° | D、150° |