题目内容
13.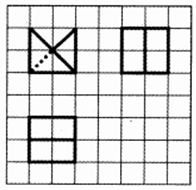 如图所示,网格纸上小正方形的边长为$\frac{1}{2}$,粗实线及粗虚线画出的是某几何体的三视图,则两个这样的几何体拼接而成的几何体表面积最小值为( )
如图所示,网格纸上小正方形的边长为$\frac{1}{2}$,粗实线及粗虚线画出的是某几何体的三视图,则两个这样的几何体拼接而成的几何体表面积最小值为( )| A. | 5+2$\sqrt{2}$ | B. | 6+2$\sqrt{2}$ | C. | 5 | D. | 6 |
分析 由三视图可知:该几何体为两个三棱柱组成的.则两个这样的几何体拼接而成的几何体表面积最小值时为正方体.
解答 解:由三视图可知:该几何体为两个全等的直三棱柱组成的.
则两个这样的几何体拼接而成的几何体表面积最小值时为正方体:
因此最小表面积=12×6=6.
故选:D.
点评 本题考查了直三棱柱、正方体的三视图、面积计算公式,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案
相关题目
4.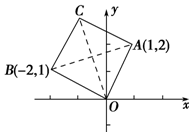 如图在复平面上,一个正方形的三个顶点对应的复数分别是1+2i,-2+i,0,那么这个正方形的第四个顶点对应的复数为( )
如图在复平面上,一个正方形的三个顶点对应的复数分别是1+2i,-2+i,0,那么这个正方形的第四个顶点对应的复数为( )
 如图在复平面上,一个正方形的三个顶点对应的复数分别是1+2i,-2+i,0,那么这个正方形的第四个顶点对应的复数为( )
如图在复平面上,一个正方形的三个顶点对应的复数分别是1+2i,-2+i,0,那么这个正方形的第四个顶点对应的复数为( )| A. | 3+i | B. | -1+3i | C. | 1-3i | D. | 3-i |
1.某几何体的三视图如图所示,其正视图,侧视图,俯视图均为全等的正方形,则该几何体的体积为( )

| A. | $\frac{4}{3}$ | B. | $\frac{8}{3}$ | C. | $\sqrt{6}$ | D. | 2$\sqrt{6}$ |
5.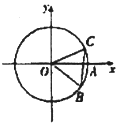 ∠AOB如图,⊙O与x轴的正半轴交点为A,点B,C在⊙O上,且$B(\frac{3}{5},-\frac{4}{5})$,点C在第一象限,∠AOC=α,BC=1,则$cos(\frac{5π}{6}-α)$=( )
∠AOB如图,⊙O与x轴的正半轴交点为A,点B,C在⊙O上,且$B(\frac{3}{5},-\frac{4}{5})$,点C在第一象限,∠AOC=α,BC=1,则$cos(\frac{5π}{6}-α)$=( )
 ∠AOB如图,⊙O与x轴的正半轴交点为A,点B,C在⊙O上,且$B(\frac{3}{5},-\frac{4}{5})$,点C在第一象限,∠AOC=α,BC=1,则$cos(\frac{5π}{6}-α)$=( )
∠AOB如图,⊙O与x轴的正半轴交点为A,点B,C在⊙O上,且$B(\frac{3}{5},-\frac{4}{5})$,点C在第一象限,∠AOC=α,BC=1,则$cos(\frac{5π}{6}-α)$=( )| A. | $-\frac{4}{5}$ | B. | $-\frac{3}{5}$ | C. | $\frac{3}{5}$ | D. | $\frac{4}{5}$ |
7.已知函数$f(x)=lnx+\frac{1}{2}{x^2}-ax+1$,下列结论中错误的是( )
| A. | 当a=2时,x=1是f(x)的一个极值点 | B. | 当-2<a<2时,函数f(x)无极值 | ||
| C. | 当a>2时,f(x)的极小值小于0 | D. | ?a∈R,f(x)必有零点 |
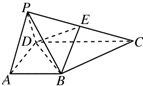 已知在四棱锥P-ABCD中,底面ABCD是直角梯形,∠BAD=90°,2AB=2AD=CD,侧面PAD是正三角形且垂直于底面ABCD,E是PC的中点.
已知在四棱锥P-ABCD中,底面ABCD是直角梯形,∠BAD=90°,2AB=2AD=CD,侧面PAD是正三角形且垂直于底面ABCD,E是PC的中点.