题目内容
5.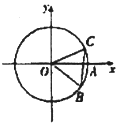 ∠AOB如图,⊙O与x轴的正半轴交点为A,点B,C在⊙O上,且$B(\frac{3}{5},-\frac{4}{5})$,点C在第一象限,∠AOC=α,BC=1,则$cos(\frac{5π}{6}-α)$=( )
∠AOB如图,⊙O与x轴的正半轴交点为A,点B,C在⊙O上,且$B(\frac{3}{5},-\frac{4}{5})$,点C在第一象限,∠AOC=α,BC=1,则$cos(\frac{5π}{6}-α)$=( )| A. | $-\frac{4}{5}$ | B. | $-\frac{3}{5}$ | C. | $\frac{3}{5}$ | D. | $\frac{4}{5}$ |
分析 方法一:由题意求得sinα,cosα的值,利用两角差的余弦展开cos($\frac{5π}{6}$-α)得答案.
方法二:根据角的变化得到∠AOB=a-$\frac{π}{3}$,根据诱导公式即可求出答案.
解答 解:方法一:如图,由B($\frac{3}{5}$,-$\frac{4}{5}$),得OB=OC=1,又BC=1,
∴∠BOC=$\frac{π}{3}$,由三角函数的定义,得sin∠AOB=$\frac{4}{5}$,cos∠AOB=$\frac{3}{5}$.
∴sinα=sin($\frac{π}{3}$-∠AOB)=sin$\frac{π}{3}$cos∠AOB-cos$\frac{π}{3}$sin∠AOB=$\frac{\sqrt{3}}{2}$×$\frac{3}{5}$-$\frac{1}{2}$×$\frac{4}{5}$=$\frac{3\sqrt{3}-4}{10}$,
同理cosα=$\frac{3+4\sqrt{3}}{10}$
∴cos($\frac{5π}{6}$-α)=cos$\frac{5π}{6}$cosα+sin$\frac{5π}{6}$sinα=-$\frac{\sqrt{3}}{2}$×$\frac{3+4\sqrt{3}}{10}$+$\frac{1}{2}$×$\frac{3\sqrt{3}-4}{10}$=-$\frac{4}{5}$,
方法二:∵∠AOB是OA逆时针转至OC,再顺时针转至OB所得到
∴∠AOB=0+a-$\frac{π}{3}$=a-$\frac{π}{3}$
∴sin(a-$\frac{π}{4}$)=-$\frac{4}{5}$
∴cos($\frac{5π}{6}$-a)
=cos[$\frac{π}{2}$-(a-$\frac{π}{3}$)]
=sin(a-$\frac{π}{3}$)
=-$\frac{4}{5}$,
故选:A.
点评 本题考查三角函数的化简求值,考查三角函数的定义,考查两角差的正弦和余弦,是基础题.

 优加精卷系列答案
优加精卷系列答案| A. | y=2x-2-x | B. | y=cosx | C. | y=log2|x| | D. | y=x+x-1 |

| A. | $\frac{5π}{3}$ | B. | $\frac{10π}{3}$ | C. | $\frac{11π}{3}$ | D. | $\frac{22π}{3}$ |
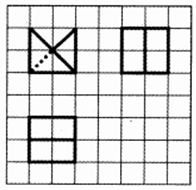 如图所示,网格纸上小正方形的边长为$\frac{1}{2}$,粗实线及粗虚线画出的是某几何体的三视图,则两个这样的几何体拼接而成的几何体表面积最小值为( )
如图所示,网格纸上小正方形的边长为$\frac{1}{2}$,粗实线及粗虚线画出的是某几何体的三视图,则两个这样的几何体拼接而成的几何体表面积最小值为( )| A. | 5+2$\sqrt{2}$ | B. | 6+2$\sqrt{2}$ | C. | 5 | D. | 6 |
| A. | $\frac{1}{3}$ | B. | -$\frac{1}{3}$ | C. | 5 | D. | 8 |
p1:|Z|=2
p2:Z2=2i
p3:Z的共轭复数为1+i
p4:Z的虚部为-1.
其中的真命题为( )
| A. | p2,p3 | B. | p1,p2 | C. | p2,p4 | D. | p3,p4 |
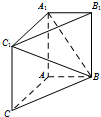 如图,在三棱柱ABC-A1B1C1中,AA1C1C是边长为4的正方形.平面ABC⊥平面AA1C1C,AB=3,BC=5.
如图,在三棱柱ABC-A1B1C1中,AA1C1C是边长为4的正方形.平面ABC⊥平面AA1C1C,AB=3,BC=5.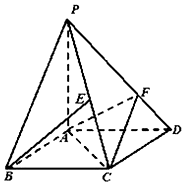 如图,四棱锥P-ABCD的底面ABCD是平行四边形,AD=2,AB=1,∠ABC=60°,PA⊥面ABCD,设E为PC中点,点F在线段PD上,且PF=2FD.
如图,四棱锥P-ABCD的底面ABCD是平行四边形,AD=2,AB=1,∠ABC=60°,PA⊥面ABCD,设E为PC中点,点F在线段PD上,且PF=2FD.