题目内容
6.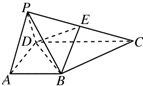 已知在四棱锥P-ABCD中,底面ABCD是直角梯形,∠BAD=90°,2AB=2AD=CD,侧面PAD是正三角形且垂直于底面ABCD,E是PC的中点.
已知在四棱锥P-ABCD中,底面ABCD是直角梯形,∠BAD=90°,2AB=2AD=CD,侧面PAD是正三角形且垂直于底面ABCD,E是PC的中点.(1)求证:BE⊥平面PCD;
(2)在PB上是否存在一点F,使AF∥平面BDE?
分析 (1)以AD的中点O为坐标原点,建立如图所示的空间直角坐标系,求出$\overrightarrow{BE}$•$\overrightarrow{PC}$=(-$\frac{3}{2}$,0,$\frac{\sqrt{3}}{2}$)•(-1,4,-$\sqrt{3}$)=0,$\overrightarrow{BE}$•$\overrightarrow{CD}$=(-$\frac{3}{2}$,0,$\frac{\sqrt{3}}{2}$)•(0,-4,0)=0,即可证明:BE⊥平面PCD;
(2)求出平面BDE的法向量,取PB中点F,证明$\overrightarrow{AF}$⊥$\overrightarrow{n}$,即可证明AF∥平面BDE.
解答 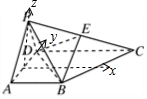 (1)证明:以AD的中点O为坐标原点,建立如图所示的空间直角坐标系.
(1)证明:以AD的中点O为坐标原点,建立如图所示的空间直角坐标系.
设AB=AD=2,则有B(1,2,0),C(-1,4,0),D(-1,0,0),P(0,0,$\sqrt{3}$),E(-$\frac{1}{2}$,2,$\frac{\sqrt{3}}{2}$),
∴$\overrightarrow{BE}$=(-$\frac{3}{2}$,0,$\frac{\sqrt{3}}{2}$),$\overrightarrow{PC}$=(-1,4,-$\sqrt{3}$),
$\overrightarrow{CD}$=(0,-4,0),
∴$\overrightarrow{BE}$•$\overrightarrow{PC}$=(-$\frac{3}{2}$,0,$\frac{\sqrt{3}}{2}$)•(-1,4,-$\sqrt{3}$)=0,
$\overrightarrow{BE}$•$\overrightarrow{CD}$=(-$\frac{3}{2}$,0,$\frac{\sqrt{3}}{2}$)•(0,-4,0)=0.
即BE⊥PC,BE⊥CD.
又PC∩CD=C,∴BE⊥平面PCD.
(2)解:设平面BDE的法向量为$\overrightarrow{n}$=(x,y,z),
则$\left\{\begin{array}{l}{-\frac{3}{2}x+\frac{\sqrt{3}}{2}z=0}\\{\frac{1}{2}x+2y+\frac{\sqrt{3}}{2}z=0}\end{array}\right.$,
令y=-1,则x=1,z=$\sqrt{3}$.
∴平面BDE的一个法向量为$\overrightarrow{n}$=(1,-1,$\sqrt{3}$).
取PB中点F,则有F($\frac{1}{2}$,1,$\frac{\sqrt{3}}{2}$).
又A(1,0,0),∴$\overrightarrow{AF}$=(-$\frac{1}{2}$,1,$\frac{\sqrt{3}}{2}$),
∵$\overrightarrow{AF}$•$\overrightarrow{n}$=(-$\frac{1}{2}$,1,$\frac{\sqrt{3}}{2}$)•(1,-1,$\sqrt{3}$)
=-$\frac{1}{2}$-1+$\frac{3}{2}$=0,
∴$\overrightarrow{AF}$⊥$\overrightarrow{n}$.
又$\overrightarrow{n}$是平面BDE的法向量,且AF?平面BDE,
∴AF∥平面BDE.
故存在PB中点F使AF∥平面BDE.
点评 本题考查线面平行,考查线面垂直的判定,考查空间向量知识的运用,属于中档题.

| A. | 2 | B. | -2 | C. | $\frac{1}{2}$ | D. | $-\frac{1}{2}$ |
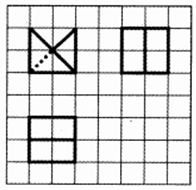 如图所示,网格纸上小正方形的边长为$\frac{1}{2}$,粗实线及粗虚线画出的是某几何体的三视图,则两个这样的几何体拼接而成的几何体表面积最小值为( )
如图所示,网格纸上小正方形的边长为$\frac{1}{2}$,粗实线及粗虚线画出的是某几何体的三视图,则两个这样的几何体拼接而成的几何体表面积最小值为( )| A. | 5+2$\sqrt{2}$ | B. | 6+2$\sqrt{2}$ | C. | 5 | D. | 6 |
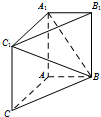 如图,在三棱柱ABC-A1B1C1中,AA1C1C是边长为4的正方形.平面ABC⊥平面AA1C1C,AB=3,BC=5.
如图,在三棱柱ABC-A1B1C1中,AA1C1C是边长为4的正方形.平面ABC⊥平面AA1C1C,AB=3,BC=5.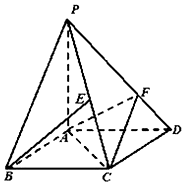 如图,四棱锥P-ABCD的底面ABCD是平行四边形,AD=2,AB=1,∠ABC=60°,PA⊥面ABCD,设E为PC中点,点F在线段PD上,且PF=2FD.
如图,四棱锥P-ABCD的底面ABCD是平行四边形,AD=2,AB=1,∠ABC=60°,PA⊥面ABCD,设E为PC中点,点F在线段PD上,且PF=2FD.