题目内容
3.证明:若函数f(x)在区间[a,b]上是增函数,那么方程f(x)=0在区间[a,b]上至多只有一个实数根.分析 利用反证法结合函数的单调性,推出结果即可.
解答 证明:假设方程f(x)=0在区间[a,b]上至少有两个不同的实数根α,β,
即f(α)=f(β)=0.
不妨设α<β,
由于函数f(x)在区间[a,b]上是增函数,故f(α)<f(β),
这与f(α)=f(β)=0矛盾,
所以方程f(x)=0在区间[a,b]上至多只有一个实数根.
点评 本题考查函数的零点判定定理以及反证法的应用,考查转化思想以及计算能力.

练习册系列答案
 黄冈360度定制密卷系列答案
黄冈360度定制密卷系列答案 阳光考场单元测试卷系列答案
阳光考场单元测试卷系列答案 名校联盟冲刺卷系列答案
名校联盟冲刺卷系列答案 名校提分一卷通系列答案
名校提分一卷通系列答案
相关题目
11.已知抛物线C:y2=8x,点P为抛物线上任意一点,过点P向圆D:x2+y2-4x+3=0作切线,切点分别为A,B,则四边形PADB面积的最小值为( )
| A. | $\sqrt{2}$ | B. | $\sqrt{3}$ | C. | 2 | D. | 3 |
15.下列函数中,既是偶函数,又在区间(0,3)内是减函数的是( )
| A. | y=2x-2-x | B. | y=cosx | C. | y=log2|x| | D. | y=x+x-1 |
12.设函数$f(x)=\left\{\begin{array}{l}{log_{\frac{1}{2}}}(x+1),0≤x≤1\\ f(x-1),x>1\end{array}\right.$,则$f(\sqrt{2})$的值是( )
| A. | 2 | B. | -2 | C. | $\frac{1}{2}$ | D. | $-\frac{1}{2}$ |
13.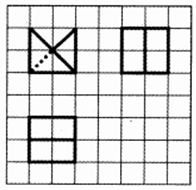 如图所示,网格纸上小正方形的边长为$\frac{1}{2}$,粗实线及粗虚线画出的是某几何体的三视图,则两个这样的几何体拼接而成的几何体表面积最小值为( )
如图所示,网格纸上小正方形的边长为$\frac{1}{2}$,粗实线及粗虚线画出的是某几何体的三视图,则两个这样的几何体拼接而成的几何体表面积最小值为( )
 如图所示,网格纸上小正方形的边长为$\frac{1}{2}$,粗实线及粗虚线画出的是某几何体的三视图,则两个这样的几何体拼接而成的几何体表面积最小值为( )
如图所示,网格纸上小正方形的边长为$\frac{1}{2}$,粗实线及粗虚线画出的是某几何体的三视图,则两个这样的几何体拼接而成的几何体表面积最小值为( )| A. | 5+2$\sqrt{2}$ | B. | 6+2$\sqrt{2}$ | C. | 5 | D. | 6 |
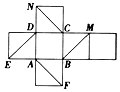 如图是正方体的平面展开图.关于这个正方体,有以下判断:①EC⊥平面AFN;
如图是正方体的平面展开图.关于这个正方体,有以下判断:①EC⊥平面AFN;