题目内容
1．某几何体的三视图如图所示，其正视图，侧视图，俯视图均为全等的正方形，则该几何体的体积为（ ）
| A． | $\frac{4}{3}$ | B． | $\frac{8}{3}$ | C． | $\sqrt{6}$ | D． | 2$\sqrt{6}$ |
分析 该几何体为正八面体，即两个全等的正四棱锥，棱长为$\sqrt{2}$，棱锥的高为1，即可求出体积
解答 解：该几何体为正八面体，即两个全等的正四棱锥，棱长为$\sqrt{2}$，棱锥的高为1，
所以，其体积为：2×$\frac{1}{3}$（$\sqrt{2}$×$\sqrt{2}$）×1=$\frac{4}{3}$，
故选：A
点评 本题考查的知识点棱锥的体积和表面积，空间几何体的三视图．
练习册系列答案
相关题目
11．已知抛物线C：y2=8x，点P为抛物线上任意一点，过点P向圆D：x2+y2-4x+3=0作切线，切点分别为A，B，则四边形PADB面积的最小值为（ ）
| A． | $\sqrt{2}$ | B． | $\sqrt{3}$ | C． | 2 | D． | 3 |
12．设函数$f（x）=\left\{\begin{array}{l}{log_{\frac{1}{2}}}（x+1），0≤x≤1\\ f（x-1），x＞1\end{array}\right.$，则$f（\sqrt{2}）$的值是（ ）
| A． | 2 | B． | -2 | C． | $\frac{1}{2}$ | D． | $-\frac{1}{2}$ |
16．某空间几何体的三视图如图所示，则此几何体的体积为（ ）
| A． | $\frac{5π}{3}$ | B． | $\frac{10π}{3}$ | C． | $\frac{11π}{3}$ | D． | $\frac{22π}{3}$ |
13．
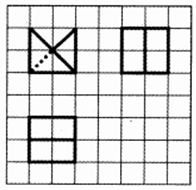如图所示，网格纸上小正方形的边长为$\frac{1}{2}$，粗实线及粗虚线画出的是某几何体的三视图，则两个这样的几何体拼接而成的几何体表面积最小值为（ ）
如图所示，网格纸上小正方形的边长为$\frac{1}{2}$，粗实线及粗虚线画出的是某几何体的三视图，则两个这样的几何体拼接而成的几何体表面积最小值为（ ）| A． | 5+2$\sqrt{2}$ | B． | 6+2$\sqrt{2}$ | C． | 5 | D． | 6 |