题目内容
4．
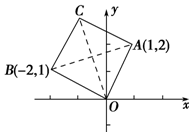如图在复平面上，一个正方形的三个顶点对应的复数分别是1+2i，-2+i，0，那么这个正方形的第四个顶点对应的复数为（ ）| A． | 3+i | B． | -1+3i | C． | 1-3i | D． | 3-i |
分析 利用复数的几何意义、向量的平行四边形法则即可得出．
解答 解：∵$\overrightarrow{OC}=\overrightarrow{OA}+\overrightarrow{OB}$，
∴$\overrightarrow{OC}$对应的复数为：1+2i-2+i=-1+3i，
∴点C对应的复数为-1+3i．
故选：B．
点评 本题考查了复数的几何意义、向量的平行四边形法则，考查了推理能力与计算能力，属于基础题．
练习册系列答案
阅读快车系列答案
相关题目
15．下列函数中，既是偶函数，又在区间（0，3）内是减函数的是（ ）
| A． | y=2x-2-x | B． | y=cosx | C． | y=log2|x| | D． | y=x+x-1 |
12．设函数$f（x）=\left\{\begin{array}{l}{log_{\frac{1}{2}}}（x+1），0≤x≤1\\ f（x-1），x＞1\end{array}\right.$，则$f（\sqrt{2}）$的值是（ ）
| A． | 2 | B． | -2 | C． | $\frac{1}{2}$ | D． | $-\frac{1}{2}$ |
如图所示的三角形数阵角“莱布尼兹调和三角形”，它是由整数的倒数组成的，第n行有n个数，且两端的数均为$\frac{1}{n}（{n≥2}）$，每个数使它下一行左右相邻两个数的和，如$\frac{1}{1}=\frac{1}{2}+\frac{1}{2}，\frac{1}{2}=\frac{1}{3}+\frac{1}{6}，\frac{1}{3}=\frac{1}{4}+\frac{1}{12}$，则第7行第5个数（从左到右）为$\frac{1}{105}$．
16．某空间几何体的三视图如图所示，则此几何体的体积为（ ）
| A． | $\frac{5π}{3}$ | B． | $\frac{10π}{3}$ | C． | $\frac{11π}{3}$ | D． | $\frac{22π}{3}$ |
13．
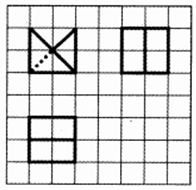如图所示，网格纸上小正方形的边长为$\frac{1}{2}$，粗实线及粗虚线画出的是某几何体的三视图，则两个这样的几何体拼接而成的几何体表面积最小值为（ ）
如图所示，网格纸上小正方形的边长为$\frac{1}{2}$，粗实线及粗虚线画出的是某几何体的三视图，则两个这样的几何体拼接而成的几何体表面积最小值为（ ）| A． | 5+2$\sqrt{2}$ | B． | 6+2$\sqrt{2}$ | C． | 5 | D． | 6 |
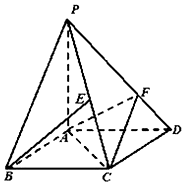如图，四棱锥P-ABCD的底面ABCD是平行四边形，AD=2，AB=1，∠ABC=60°，PA⊥面ABCD，设E为PC中点，点F在线段PD上，且PF=2FD．