题目内容
8.(文科)等差数列{an}的首项a1=3,a5=11,bn=an-12(1)求an和{ bn}的前n项和Sn;
(2)若Tn=|b1|+|b2|+…+|bn|,求Tn;
(3)设cn=$\frac{1}{{{a_n}{a_{n+1}}}}$,求数列{cn}的前n项和Rn.
分析 (1)利用等差数列的通项公式可得an,再利用等差数列的求和公式可得数列{ bn}的前n项和Sn.
(2)令bn=2n-11≤0,解得n≤5.n≤5时,Tn=-b1-…-bn=-Sn.n≥6时,Tn=-b1-…-b5+b6+…+bn=-2S5+Sn.
(3)cn=$\frac{1}{{{a_n}{a_{n+1}}}}$=$\frac{1}{(2n+1)(2n+3)}$=$\frac{1}{2}(\frac{1}{2n+1}-\frac{1}{2n+3})$,利用“裂项求和”方法即可得出.
解答 解:(1)等差数列{an}的首项a1=3,a5=11,设公差为d,则3+4d=11,解得d=2.
∴an=3+2(n-1)=2n+1.
bn=an-12=2n-11.
数列{ bn}的前n项和Sn=$\frac{n(-9+2n-11)}{2}$=n2-10n.
(2)令bn=2n-11≤0,解得n≤5.
∴n≤5时,Tn=-b1-…-bn=-Sn=-n2+10n.
n≥6时,Tn=-b1-…-b5+b6+…+bn=-2S5+Sn=n2-10n-2×(25-50)=n2-10n+50.
综上可得:Tn=$\left\{\begin{array}{l}{-{n}^{2}+10n,n≤5}\\{{n}^{2}-10n+50,n≥6}\end{array}\right.$.
(3)cn=$\frac{1}{{{a_n}{a_{n+1}}}}$=$\frac{1}{(2n+1)(2n+3)}$=$\frac{1}{2}(\frac{1}{2n+1}-\frac{1}{2n+3})$,
数列{cn}的前n项和Rn=$\frac{1}{2}[(\frac{1}{3}-\frac{1}{5})+(\frac{1}{5}-\frac{1}{7})$+…+$(\frac{1}{2n+1}-\frac{1}{2n+3})]$
=$\frac{1}{2}(\frac{1}{3}-\frac{1}{2n+3})$=$\frac{n}{2n+3}$.
点评 本题考查了数列递推关系、“裂项求和”方法、等差数列的通项公式与求和公式、分类讨论方法,考查了推理能力与计算能力,属于中档题.


| A. | $\frac{5π}{3}$ | B. | $\frac{10π}{3}$ | C. | $\frac{11π}{3}$ | D. | $\frac{22π}{3}$ |
| A. | $\frac{2}{3}$ | B. | $-\frac{2}{3}$ | C. | $\frac{3}{2}$ | D. | $-\frac{3}{2}$ |
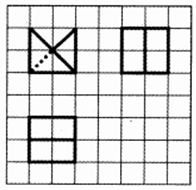 如图所示,网格纸上小正方形的边长为$\frac{1}{2}$,粗实线及粗虚线画出的是某几何体的三视图,则两个这样的几何体拼接而成的几何体表面积最小值为( )
如图所示,网格纸上小正方形的边长为$\frac{1}{2}$,粗实线及粗虚线画出的是某几何体的三视图,则两个这样的几何体拼接而成的几何体表面积最小值为( )| A. | 5+2$\sqrt{2}$ | B. | 6+2$\sqrt{2}$ | C. | 5 | D. | 6 |
| A. | $\frac{1}{3}$ | B. | -$\frac{1}{3}$ | C. | 5 | D. | 8 |
 如图所示的三角形数阵角“莱布尼兹调和三角形”,它是由整数的倒数组成的,第n行有n个数,且两端的数均为$\frac{1}{n}({n≥2})$,每个数使它下一行左右相邻两个数的和,如$\frac{1}{1}=\frac{1}{2}+\frac{1}{2},\frac{1}{2}=\frac{1}{3}+\frac{1}{6},\frac{1}{3}=\frac{1}{4}+\frac{1}{12}$,则第7行第5个数(从左到右)为$\frac{1}{105}$.
如图所示的三角形数阵角“莱布尼兹调和三角形”,它是由整数的倒数组成的,第n行有n个数,且两端的数均为$\frac{1}{n}({n≥2})$,每个数使它下一行左右相邻两个数的和,如$\frac{1}{1}=\frac{1}{2}+\frac{1}{2},\frac{1}{2}=\frac{1}{3}+\frac{1}{6},\frac{1}{3}=\frac{1}{4}+\frac{1}{12}$,则第7行第5个数(从左到右)为$\frac{1}{105}$.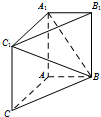 如图,在三棱柱ABC-A1B1C1中,AA1C1C是边长为4的正方形.平面ABC⊥平面AA1C1C,AB=3,BC=5.
如图,在三棱柱ABC-A1B1C1中,AA1C1C是边长为4的正方形.平面ABC⊥平面AA1C1C,AB=3,BC=5.