题目内容
已知f(x),g(x)都是定义在R上的函数,g(x)≠0,f′(x)g(x)<f(x)g′(x),f(x)=ax•g(x),(a>0,且a≠1),
+
=
,在有穷数列{
}(n=1,2,…10)中,任意取正整数k(1≤k≤10),则前k项和大于
地概率是( )
| f(1) |
| g(1) |
| f(-1) |
| g(-1) |
| 5 |
| 2 |
| f(n) |
| g(n) |
| 15 |
| 16 |
A、
| ||
B、
| ||
C、
| ||
D、
|
考点:古典概型及其概率计算公式
专题:概率与统计
分析:由f(x)=ax•g(x),得ax=
,得到y=ax为减函数,由
+
=
,解得a=
,1-(
)n>
,得n>4,问题得以解决
| f(x) |
| g(x) |
| f(1) |
| g(1) |
| f(-1) |
| g(-1) |
| 5 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 15 |
| 16 |
解答:
解:由f(x)=ax•g(x),得ax=
,
又(
)′=
<0
∴y=ax为减函数,则0<a<1,
由
+
=
,得a+
=
,
解得a=
,
∴
=
,
∴
+
+…+
=1-(
)n,
由1-(
)n>
,得n>4.
∴前k项和大于
的概率为P=
=
.
故选:C
| f(x) |
| g(x) |
又(
| f(x) |
| g(x) |
| f′(x)+g(x)-f(x)g′(x) |
| g2(x) |
∴y=ax为减函数,则0<a<1,
由
| f(1) |
| g(1) |
| f(-1) |
| g(-1) |
| 5 |
| 2 |
| 1 |
| a |
| 5 |
| 2 |
解得a=
| 1 |
| 2 |
∴
| f(n) |
| g(n) |
| 1 |
| 2n |
∴
| 1 |
| 2 |
| 1 |
| 22 |
| 1 |
| 2n |
| 1 |
| 2 |
由1-(
| 1 |
| 2 |
| 15 |
| 16 |
∴前k项和大于
| 15 |
| 16 |
| 6 |
| 10 |
| 3 |
| 5 |
故选:C
点评:考查学生对导数、指数函数的单调性、等比数列求和、古典概型等有关知识的掌握与应用能力,属于中档题

练习册系列答案
相关题目
已知一正方形的两顶点为双曲线C的两焦点,若另外两个项点在双曲线C上,则双曲线C的离心率e=( )
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
2011年西安世园会组委会要从五名志愿者中选派四人分别从事翻译、导游、礼仪、司机四项不同的工作,若其中有一名志愿者只能从事司机工作,其余四人均能从事这四项工作,则不同的选派方案共有( )
| A、240种 | B、36种 |
| C、24种 | D、48种 |
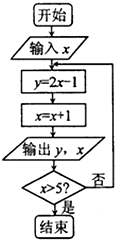 如程序框图所示已知集合A={x|框图中输出的x值},集合B={y|框图中输出的y值},当x=1时A∩B=( )
如程序框图所示已知集合A={x|框图中输出的x值},集合B={y|框图中输出的y值},当x=1时A∩B=( )| A、∅ | B、{3} |
| C、{1,3,5} | D、{3,5} |