Question

设F₁，F₂分别是双曲线C：

x2

a2

-

y2

b2

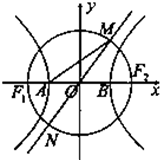
=1（a＞0，b＞0）的左右焦点，A为双曲线的左顶点，以F₁，F₂为为直径的圆交双曲线的某条渐近线于MN两点（M在x轴上方，N在x轴下方），c为双曲线的半焦距，O为坐标原点．则下列命题正确的是

 

（写出所有正确命题的编号）．
①|OM|=|ON|=c；
②点N的坐标为（a，b）；
③∠MAN＞90°；
④若∠MAN=120°，则双曲线C的离心率为

21

3

；
⑤若∠MAN=120°，且△AMN的面积为2

3

，则双曲线C的方程为

x2

3

-

y2

4

=1．

Answer 1

考点：双曲线的简单性质

专题：计算题,直线与圆,圆锥曲线的定义、性质与方程

分析：由圆的方程和双曲线的性质，即可判断①；求出渐近线与圆的交点，即可判断②；求出向量AM，AN的坐标，再由数量积即可判断③；再利用余弦定理，求出a，c之间的关系，即可得出双曲线的离心率，即可判断④；由④，运用三角形的面积公式，结合a，b，c的关系，解得a，b，即可判断⑤．

解答： 解：对于①，由以F₁，F₂为为直径的圆
交双曲线的某条渐近线于MN两点，
则|OM|=|ON|=c正确；
对于②，令渐近线方程为y=

b

a

x，
代入圆x²+y²=c²=a²+b²，解得，M（a，b），N（-a，-b），
则②错误；
对于③，由于A（-a，0），M（a，b），N（-a，-b），

AM

=（2a，b），

AN

=（0，-b），

AM

•

AN

=-b²＜0，则∠MAN＞90°正确；
对于④，M（a，b），N（-a，-b）；又∵A（-a，0），且∠MAN=120°，
∴由余弦定理得4c²=（a+a）²+b²+b²-2

(a+a)2+b2

•bcos 120°，
化简得7a²=3c²，∴e=

c

a

=

21

3

．④正确；
对于⑤，由④得e=

c

a

=

21

3

，△AMN的面积为2

3

，则有

1

2

ab×2=2

3

，
再由a²+b²=c²，解得，a=

3

，b=2，即有双曲线C的方程为

x2

3

-

y2

4

=1．则⑤正确．
故答案为：①③④⑤．

点评：本题考查双曲线的方程和性质，考查离心率的求法和直线与圆相交，考查运算能力，属于中档题和易错题．