题目内容
9.已知函数g(x)=ax2-2ax+1+b(a>0)在区间[2,3]上的最大值为4,最小值为1,记f(x)=g(|x|)(1)求实数a、b的值;
(2)若不等式$f({log_2}k)>f(\frac{3}{2})$成立,求实数k的取值范围;
(3)对于任意满足p=x0<x1<x2<…<xn-1<xn=q(n∈N,n≥3)的自变量x0,x1,x2,…,xn-1,xn,如果存在一个常数M>0,使得定义在区间[p,q]上的一个函数m(x),有|m(x1)-m(x0)|+|m(x2)-m(x1)|+…+|m(xn)-m(xn-1)|≤M恒成立,则称m(x)为区间[p,q]上的有界变差函数,试判断f(x)是否区间[0,3]上的有界变差函数,若是,求出M的最小值;若不是,请说明理由.
分析 (1)由g(x)的对称轴x=1得g(x)在区间[2,3]上是增函数,得方程组求出a,b即可;
(2)由(1)求出f(x)的表达式,解不等式求出即可;
(3)由f(x)的表达式得f(x)为[0,3]上的单调递增函数,根据有界变差函数的概念求出即可.
解答 解:(1)∵g(x)=a(x-1)2+1+b-a,
又a>0,∴g(x)在区间[2,3]上是增函数,
故g(2)=1,g(3)=4,
解得:a=1,b=0.
(2)由(1)得:g(x)=x2-2x+1,
故f(x)=x2-2|x|+1是偶函数,
∴不等式$f({log_2}k)>f(\frac{3}{2})$可化为|log2k|>$\frac{3}{2}$,
解得:k∈(0,$\frac{\sqrt{2}}{4}$)∪(2$\sqrt{2}$,+∞).
(3)∵f(x)=$\left\{\begin{array}{l}{{x}^{2}-2x+1,x≥1}\\{{x}^{2}+2x+1,x<1}\end{array}\right.$,
∴f(x)为[0,1]上单调递减,[1,3]上的单调递增函数,
则对于任意满足1=x0<x1<x2<…<xn-1<xn=3(n∈N*,n≥3)的自变量x0,x1,x2,…,xn,
有f(1)=f(x0)<f(x1)<f(x2)<…<f(xn-1)<f(xn)=f(3),
∴|f(x1)-f(x0)|+|f(x2)-f(x1)|+…+|f(xn)-f(xn-1)|
=f(x1)-f(x0)+f(x2)-f(x1)+…+f(xn)-f(xn-1)
=f(xn)-f(xn-1)
=f(3)-f(1)
=4,
∴存在常数M≥4,使得|m(x1)-m(x0)|+|m(x2)-m(x1)|+…+|m(xn)-m(xn-1)|≤M.
函数f(x)为区间[0,3]上的有界变差函数.即M的最小值为4.
点评 本题考查函数的性质,导数的应用,函数的单调性,新概念问题,是一道综合题.

 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案| A. | [2,+∞) | B. | (2,+∞) | C. | [$\sqrt{2}$,+∞) | D. | ($\sqrt{2}$,+∞) |
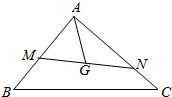 如图所示,已知点G是△ABC的重心,过点G作直线与AB,AC两边分别交于M,N两点,且$\overrightarrow{AM}$=x$\overrightarrow{AB}$,$\overrightarrow{AN}$=y$\overrightarrow{AC}$,则x+2y的最小值为( )
如图所示,已知点G是△ABC的重心,过点G作直线与AB,AC两边分别交于M,N两点,且$\overrightarrow{AM}$=x$\overrightarrow{AB}$,$\overrightarrow{AN}$=y$\overrightarrow{AC}$,则x+2y的最小值为( )| A. | 2 | B. | $\frac{1}{3}$ | C. | $\frac{{3+2\sqrt{2}}}{3}$ | D. | $\frac{3}{4}$ |
| A. | (8,+∞) | B. | (-∞,0)∪(8,+∞) | C. | (0,8) | D. | (-∞,0)∪(0,8) |
| A. | 2015+2016i | B. | 2015-2016i | C. | -2016+2015i | D. | -2016-2015i |
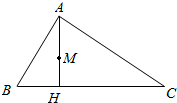 如图,在△ABC中,AB=2,BC=3,∠ABC=60°,AH⊥BC于点H,M为AH的中点,若$\overrightarrow{AM}$=λ$\overrightarrow{AB}$+μ$\overrightarrow{BC}$,则λ+μ=$\frac{2}{3}$.
如图,在△ABC中,AB=2,BC=3,∠ABC=60°,AH⊥BC于点H,M为AH的中点,若$\overrightarrow{AM}$=λ$\overrightarrow{AB}$+μ$\overrightarrow{BC}$,则λ+μ=$\frac{2}{3}$.