题目内容
14.已知函数f(x)=$\left\{\begin{array}{l}{3^{x+1}}(x≤0)\\{log_2}x(x>0)\end{array}$,则不等式f(x)>3的解集为( )| A. | (8,+∞) | B. | (-∞,0)∪(8,+∞) | C. | (0,8) | D. | (-∞,0)∪(0,8) |
分析 根据指数不等式和对数不等式的性质进行求解即可.
解答 解:若x≤0,则由f(x)>3得3x+1>3,即x+1>1,即x>0,此时不等式无解,
若x>0,则由f(x)>3得log2x>3,即x>8,此时x>8,
即不等式的解集为,(8,+∞),
故选:A
点评 本题主要考查不等式的求解,根据分段函数的不等式,结合指数不等式和对数不等式的性质进行求解是解决本题的关键.

练习册系列答案
相关题目
2.已知f(x)是偶函数,它在[0,+∞)上是减函数,若f(lgx)>f(2),则x的取值范围是( )
| A. | $(\frac{1}{100},1)$ | B. | (0,$\frac{1}{100}$)∪(1,+∞) | C. | $(\frac{1}{100},100)$ | D. | (0,1)∪(100,+∞) |
19.下列叙述错误的是( )
| A. | 若事件A发生的概率为P(A),则0≤P(A)≤1 | |
| B. | 系统抽样是不放回抽样,每个个体被抽到的可能性相等 | |
| C. | 线性回归直线$\hat y=\hat bx+\hat a$必过点$(\overline x,\overline y)$ | |
| D. | 对于任意两个事件A和B,都有P(A∪B)=P(A)+P(B) |
6.正三棱锥P-ABC中,(△ABC是正三角形,点P在平面ABC的射影是△ABC的中心)侧棱PA与底面ABC成60°角,若AB=2$\sqrt{3}$,则P到平面ABC的距离是2$\sqrt{3}$.
3.一质点按规律S(t)=2t3+1运动,则t=1时的瞬时速度为( )
| A. | 6 | B. | 5 | C. | 4 | D. | 3 |
4.正三棱柱ABC-A1B1C1各棱长均为1,M为CC1的中点,则点B1到截面A1BM的距离为( )
| A. | $\sqrt{2}$ | B. | $\frac{\sqrt{2}}{2}$ | C. | $\frac{1}{2}$ | D. | $\frac{\sqrt{3}}{2}$ |
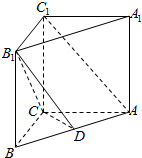 直棱柱ABC-A1B1C1中,AB=5,AC=4,BC=3,AA1=4,点D在AB上.
直棱柱ABC-A1B1C1中,AB=5,AC=4,BC=3,AA1=4,点D在AB上.