题目内容
1.已知p:A={x|x2-(a+1)x+a≤0},q:B={x|x2-3x+2≤0},若p是q的充分而不必要条件,求实数a的取值范围.分析 分别求出关于p,q的不等式的解集,根据充分必要条件的定义,判断即可.
解答 解:关于p:A={x|x2-(a+1)x+a≤0},
a<1时:A=[a,1],a≥1时:A=[1,a],
关于q:B={x|x2-3x+2≤0},
∴B=[1,2],
若p是q的充分而不必要条件,
则1≤a<2.
点评 本题考查了充分必要条件,考查不等式问题,是一道基础题.

练习册系列答案
相关题目
12.一个几何体被切割后剩下部分的几何体的三视图如图所示,则该几何体的表面积为( )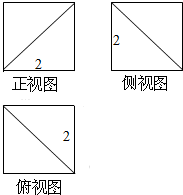

| A. | 18 | B. | 20 | C. | $18+2\sqrt{3}$ | D. | $18+4\sqrt{3}$ |
16.设f(x)=$\left\{\begin{array}{l}{x-2,(x≥10)}\\{f[f(x+6)],(x<10)}\end{array}\right.$,则f(4)的值为( )
| A. | 10 | B. | 11 | C. | 12 | D. | 13 |
6.正三棱锥P-ABC中,(△ABC是正三角形,点P在平面ABC的射影是△ABC的中心)侧棱PA与底面ABC成60°角,若AB=2$\sqrt{3}$,则P到平面ABC的距离是2$\sqrt{3}$.
13.已知集合M={x|x≥-$\frac{1}{2}$},N={x|1-x2≥0},则∁R(M∪N)=( )
| A. | (-∞,-1] | B. | (-∞,-1) | C. | (-1,+∞) | D. | [-1,+∞) |