题目内容
18.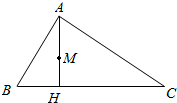 如图,在△ABC中,AB=2,BC=3,∠ABC=60°,AH⊥BC于点H,M为AH的中点,若$\overrightarrow{AM}$=λ$\overrightarrow{AB}$+μ$\overrightarrow{BC}$,则λ+μ=$\frac{2}{3}$.
如图,在△ABC中,AB=2,BC=3,∠ABC=60°,AH⊥BC于点H,M为AH的中点,若$\overrightarrow{AM}$=λ$\overrightarrow{AB}$+μ$\overrightarrow{BC}$,则λ+μ=$\frac{2}{3}$.
分析 由题意可得$\overrightarrow{BH}$=$\frac{1}{3}$$\overrightarrow{BC}$,从而由$\overrightarrow{AH}$=$\overrightarrow{AB}$+$\overrightarrow{BH}$,$\overrightarrow{AM}$=$\frac{1}{2}$$\overrightarrow{AH}$解得λ+μ.
解答 解:∵AB=2,∠ABC=60°,
∴BH=1,
∴$\overrightarrow{BH}$=$\frac{1}{3}$$\overrightarrow{BC}$,
∴$\overrightarrow{AH}$=$\overrightarrow{AB}$+$\overrightarrow{BH}$=$\overrightarrow{AB}$+$\frac{1}{3}$$\overrightarrow{BC}$,
∴$\overrightarrow{AM}$=$\frac{1}{2}$$\overrightarrow{AH}$=$\frac{1}{2}$($\overrightarrow{AB}$+$\frac{1}{3}$$\overrightarrow{BC}$)=$\frac{1}{2}$$\overrightarrow{AB}$+$\frac{1}{6}$$\overrightarrow{BC}$=λ$\overrightarrow{AB}$+μ$\overrightarrow{BC}$,
故λ=$\frac{1}{2}$,μ=$\frac{1}{6}$,故λ+μ=$\frac{2}{3}$;
故答案为:$\frac{2}{3}$.
点评 本题考查了平面向量的线性运算的应用及平面向量基本定理的应用.

| A. | (-∞,-1] | B. | (-∞,-1) | C. | (-1,+∞) | D. | [-1,+∞) |
| A. | 6 | B. | 5 | C. | 4 | D. | 3 |
| A. | p∧q | B. | ?p∧?q | C. | ?p∧q | D. | p∧?q |