题目内容
17.已知g(x)=ex(cosx+a)(a∈R)是R上的增函数,则实数a的取值范围为( )| A. | [2,+∞) | B. | (2,+∞) | C. | [$\sqrt{2}$,+∞) | D. | ($\sqrt{2}$,+∞) |
分析 求函数的导数,要使函数单调递增,则f′(x)≥0立,然后求出实数a的取值范围.
解答 解:因为f(x)=ex(cosx+a),所以f′(x)=ex(cosx+a-sinx).
要使函数单调递增,则f′(x)≥0成立.
即-sinx+a+cosx≥0恒成立.
所以a≥sinx-cosx,
因为sinx-cosx=$\sqrt{2}$sin(x-$\frac{π}{4}$)
所以-$\sqrt{2}$≤sinx-cosx≤$\sqrt{2}$,
所以a≥$\sqrt{2}$,
故选:C.
点评 本题主要考查导数的基本运算以及利用导数研究函数的单调性,注意当函数单调递增时,f'(x)≥0恒成立.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
5.函数f(x)=$\sqrt{x+1}$-ln(2-x)的定义域为( )
| A. | (2,+∞) | B. | (-1,+∞) | C. | [-1,2) | D. | (-1,2) |
12.一个几何体被切割后剩下部分的几何体的三视图如图所示,则该几何体的表面积为( )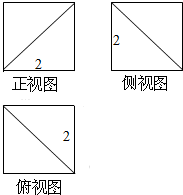

| A. | 18 | B. | 20 | C. | $18+2\sqrt{3}$ | D. | $18+4\sqrt{3}$ |
2.已知f(x)是偶函数,它在[0,+∞)上是减函数,若f(lgx)>f(2),则x的取值范围是( )
| A. | $(\frac{1}{100},1)$ | B. | (0,$\frac{1}{100}$)∪(1,+∞) | C. | $(\frac{1}{100},100)$ | D. | (0,1)∪(100,+∞) |
6.正三棱锥P-ABC中,(△ABC是正三角形,点P在平面ABC的射影是△ABC的中心)侧棱PA与底面ABC成60°角,若AB=2$\sqrt{3}$,则P到平面ABC的距离是2$\sqrt{3}$.
7.已知命题p:函数y=2-ax+1(a>0,a≠1)恒过定点(-1,1):命题q:若函数f(x-1)为偶函数,则f(x)的图象关于直线x=1对称.下列命题为真命题的是( )
| A. | p∧q | B. | ?p∧?q | C. | ?p∧q | D. | p∧?q |
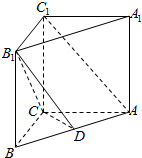 直棱柱ABC-A1B1C1中,AB=5,AC=4,BC=3,AA1=4,点D在AB上.
直棱柱ABC-A1B1C1中,AB=5,AC=4,BC=3,AA1=4,点D在AB上.