��Ŀ����
4�������P��x0��y0����ֱ��l��Ax+By+C=0��A2+B2��0�����������Ϊd=$\frac{{A{x_0}+B{y_0}+C}}{{\sqrt{{A^2}+{B^2}}}}$����֪��P1��P2��ֱ��l���������ֱ���d1��d2�������������⣺����d1=d2����ֱ��P1P2��ֱ��lƽ�У�
����d1=-d2����ֱ��P1P2��ֱ��l��ֱ��
����d1•d2��0����ֱ��P1P2��ֱ��lƽ�л��ཻ��
����d1•d2��0����ֱ��P1P2��ֱ��l�ཻ��
����������ȷ���������Ǣۢܣ�
���� �����������Ķ��壬����P��x0��y0����Ax1+By1+C�ķ��ţ��ֱ��ֱ��P1P2��ֱ��l��λ�ù�ϵ�����жϣ�
��� �⣺���ڢ٣���d1-d2=0������d1=d2����Ax1+By1+C=Ax2+By2+C��
����d1=d2=0ʱ����Ax1+By1+C=Ax2+By2+C=0��
���P1��P2����ֱ��l�����ʱֱ��P1P2��ֱ��l�غϣ���ٴ���
���ڢڣ��ɢ�֪����d1=d2=0ʱ������d1+d2=0��
����ʱAx1+By1+C=Ax2+By2+C=0��
���P1��P2����ֱ��l�����ʱֱ��P1P2��ֱ��l�غϣ���ڴ���
���ڢۣ���d1•d2��0������Ax1+By1+C����Ax2+By2+C����0��
���P1��P2�ֱ�λ��ֱ��l��ͬ�࣬��ֱ��P1P2��ֱ��l�ཻ��ƽ�У������ȷ��
���ڢܣ���d1•d2��0������Ax1+By1+C����Ax2+By2+C����0��
���P1��P2�ֱ�λ��ֱ��l�����࣬��ֱ��P1P2��ֱ��l�ཻ�������ȷ��
�ʴ�Ϊ���ۢܣ�
���� ������Ҫ������ֱ�߾����йص�������жϣ����������Ƴ�����ֱ�ߵ�λ�ù�ϵ�ǽ������Ĺؼ����ۺ��Խ�ǿ���������⣮

��ϰ��ϵ�д�
 ������������Ӧ����ϵ�д�
������������Ӧ����ϵ�д� ͬ����չ�Ķ�ϵ�д�
ͬ����չ�Ķ�ϵ�д�
�����Ŀ
12����ֱ��mx+ny-1=0����һ�����������ޣ�������
| A�� | m��0��n��0 | B�� | m��0��n��0 | C�� | m��0��n��0 | D�� | m��0��n��0 |
19����֪�߳�Ϊa������ABCD�У���ABC=60�㣬���������ضԽ���AC����ʹBD=a��������D-ABC�����Ϊ��������
| A�� | $\frac{a^3}{6}$ | B�� | $\frac{a^3}{12}$ | C�� | $\frac{{\sqrt{3}{a^3}}}{12}$ | D�� | $\frac{{\sqrt{2}{a^3}}}{12}$ |
9������ΪF1��-2��0����F2��2��0�������᳤Ϊ10����Բ�ı�����Ϊ��������
| A�� | $\frac{x^2}{100}+\frac{y^2}{96}=1$ | B�� | $\frac{x^2}{25}+\frac{y^2}{21}=1$ | C�� | $\frac{x^2}{96}+\frac{y^2}{100}=1$ | D�� | $\frac{x^2}{21}+\frac{y^2}{25}=1$ |
16����֪������ֱͬ��a��b������ͬƽ������£����н�����ȷ���ǣ�������
| A�� | ��a��b��a�Φ�����b�Φ� | B�� | ��a��b��a�ͦ�����b�ͦ� | ||
| C�� | ��a�Φ���a�Φ£����ɦ�=b����a��b | D�� | ��a�Φ������ͦ£���a�ͦ� |
18��y=cos��x+1��ͼ�������ڵ���ߵ����͵�֮��ľ����ǣ�������
| A�� | $\sqrt{{��^2}+4}$ | B�� | �� | C�� | 2 | D�� | $\sqrt{{��^2}+1}$ |
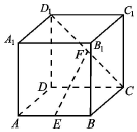 ������ABCD-A1B1C1D1�У�EΪAB�е㣬FΪCD1�е㣮
������ABCD-A1B1C1D1�У�EΪAB�е㣬FΪCD1�е㣮