题目内容
13.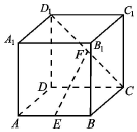 正方体ABCD-A1B1C1D1中,E为AB中点,F为CD1中点.
正方体ABCD-A1B1C1D1中,E为AB中点,F为CD1中点.(1)求证:EF∥平面ADD1A1;
(2)求直线EF和平面CDD1C1所成角的正弦值.
分析 (1)取DD1中点M,连接MA,MF,证明EF∥AM,然后证明EF∥平面ADD1A1.
(2)说明∠AMD与直线EF和平面CDD1C1所成角相等,在Rt△AMD中,解三角形求解直线EF和平面CDD1C1所成角的正弦值即可.
解答  解:(1)证明:取DD1中点M,连接MA,MF,有$MF\underline{\underline∥}AE\underline{\underline∥}\frac{1}{2}DC$,
解:(1)证明:取DD1中点M,连接MA,MF,有$MF\underline{\underline∥}AE\underline{\underline∥}\frac{1}{2}DC$,
所以AEFM是平行四边形,
所以EF∥AM,又AM?平面ADD1A1,EF?平面ADD1A1,
所以EF∥平面ADD1A1,得证.
(2)因为EF∥AM,AD⊥平面CDD1C1,所以∠AMD与直线EF和平面CDD1C1所成角相等,
又在Rt△AMD中,有$sin∠AMD=\frac{2}{{\sqrt{5}}}=\frac{{2\sqrt{5}}}{5}$,
所以直线EF和平面CDD1C1所成角的正弦值为$\frac{{2\sqrt{5}}}{5}$.
点评 本题考查直线与平面所成角,直线与平面平行的判定定理的应用,考查空间想象能力以及逻辑推理能力.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
3.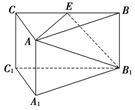 如图,三棱柱ABCA1B1C1中,侧棱AA1垂直底面A1B1C1,底面三角形A1B1C1是正三角形,E是BC中点,则下列叙述正确的是( )
如图,三棱柱ABCA1B1C1中,侧棱AA1垂直底面A1B1C1,底面三角形A1B1C1是正三角形,E是BC中点,则下列叙述正确的是( )
 如图,三棱柱ABCA1B1C1中,侧棱AA1垂直底面A1B1C1,底面三角形A1B1C1是正三角形,E是BC中点,则下列叙述正确的是( )
如图,三棱柱ABCA1B1C1中,侧棱AA1垂直底面A1B1C1,底面三角形A1B1C1是正三角形,E是BC中点,则下列叙述正确的是( )| A. | CC1与B1E是异面直线 | B. | AE与B1C1是异面直线,且AE⊥B1C1 | ||
| C. | AC⊥平面ABB1A1 | D. | A1C1∥平面AB1E |
8.直三棱柱ABC-A1B1C1中,AB=AC=AA1=2,BC=2$\sqrt{2}$,则三棱柱ABC-A1B1C1的外接球的表面积为( )
| A. | 36π | B. | 28π | C. | 16π | D. | 12π |
9.已知等比数列,则“a1>0”是“a2017>0”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
7.已知集合A={x∈N|0≤x≤5},B={x|2-x<0},则A∩(∁RB)=( )
| A. | {1} | B. | {0,1} | C. | {1,2} | D. | {0,1,2} |
 某校收集该校学生从家到学校的时间后,制作成如下的频率分布直方图:
某校收集该校学生从家到学校的时间后,制作成如下的频率分布直方图: