题目内容
14.5、8、11三数的标准差为$\sqrt{6}$.分析 先求出平均数,再求出方差,由此能求出标准差.
解答 解:5、8、11三数的平均数为:
$\overline{x}$=$\frac{1}{3}(5+8+11)$=8,
5、8、11三数的方差为:
S2=$\frac{1}{3}$[(5-8)2+(8-8)2+(11-8)2]=6,
5、8、11三数的标准差为:
S=$\sqrt{{S}^{2}}$=$\sqrt{6}$.
故答案为:$\sqrt{6}$.
点评 本题三个数的标准差的求法,是基础题,解题时要认真审题,注意方差计算公式的合理运用.

练习册系列答案
 开心蛙状元测试卷系列答案
开心蛙状元测试卷系列答案
相关题目
4.已知集合A={0,2,4,6},B={x∈N|2x<33},则集合A∩B的子集个数为( )
| A. | 8 | B. | 7 | C. | 6 | D. | 4 |
2.甲、乙两人射击比赛,两人平的概率是$\frac{1}{2}$,甲获胜的概率是$\frac{1}{3}$,则甲不输的概率为( )
| A. | $\frac{2}{5}$ | B. | $\frac{5}{6}$ | C. | $\frac{1}{6}$ | D. | $\frac{1}{3}$ |
9.下列函数中,既是偶函数又在区间(0,+∞)上单调递减的是( )
| A. | y=|x| | B. | y=x-2 | C. | y=ex-e-x | D. | y=-x+1 |
19.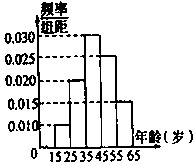 某市电视台为了宣传,举办问答活动,随机对该市15至65岁的人群进行抽样,频率分布直方图及回答问题统计结果如表所示:
某市电视台为了宣传,举办问答活动,随机对该市15至65岁的人群进行抽样,频率分布直方图及回答问题统计结果如表所示:
(1)分别求出a,b,x,y的值;
(2)从第2,3,4组回答正确的人中用分层抽样的方法抽取6人,则第2,3,4组每组应各抽取多少人?
(3)在(2)的前提下,电视台决定在所抽取的6人中随机抽取3人颁发幸运奖,求:所抽取的人中第3组至少有1人获得幸运奖的概率.
 某市电视台为了宣传,举办问答活动,随机对该市15至65岁的人群进行抽样,频率分布直方图及回答问题统计结果如表所示:
某市电视台为了宣传,举办问答活动,随机对该市15至65岁的人群进行抽样,频率分布直方图及回答问题统计结果如表所示:| 组号 | 分组 | 回答正确 的人数 | 回答正确的人数 占本组的概率 |
| 第1组 | [15,25) | 5 | 0.5 |
| 第2组 | [25,35) | a | 0.9 |
| 第3组 | [35,45) | 27 | x |
| 第4组 | [45,55) | b | 0.36 |
| 第5组 | [55,65) | 3 | y |
(2)从第2,3,4组回答正确的人中用分层抽样的方法抽取6人,则第2,3,4组每组应各抽取多少人?
(3)在(2)的前提下,电视台决定在所抽取的6人中随机抽取3人颁发幸运奖,求:所抽取的人中第3组至少有1人获得幸运奖的概率.
3.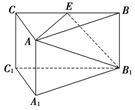 如图,三棱柱ABCA1B1C1中,侧棱AA1垂直底面A1B1C1,底面三角形A1B1C1是正三角形,E是BC中点,则下列叙述正确的是( )
如图,三棱柱ABCA1B1C1中,侧棱AA1垂直底面A1B1C1,底面三角形A1B1C1是正三角形,E是BC中点,则下列叙述正确的是( )
 如图,三棱柱ABCA1B1C1中,侧棱AA1垂直底面A1B1C1,底面三角形A1B1C1是正三角形,E是BC中点,则下列叙述正确的是( )
如图,三棱柱ABCA1B1C1中,侧棱AA1垂直底面A1B1C1,底面三角形A1B1C1是正三角形,E是BC中点,则下列叙述正确的是( )| A. | CC1与B1E是异面直线 | B. | AE与B1C1是异面直线,且AE⊥B1C1 | ||
| C. | AC⊥平面ABB1A1 | D. | A1C1∥平面AB1E |
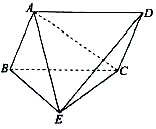 如图四棱锥E-ABCD中,四边形ABCD为平行四边形,△BCE为等边三角形,△ABE是以∠A为直角的等腰直角三角形,且AC=BC.
如图四棱锥E-ABCD中,四边形ABCD为平行四边形,△BCE为等边三角形,△ABE是以∠A为直角的等腰直角三角形,且AC=BC.