题目内容
15.满足等式cos2x-1=3cosx(x∈[0,π])的x值为$\frac{2π}{3}$.分析 利用二倍角的余弦公式解方程求得cosx的值,从而结合x∈[0,π],求得x的值.
解答 解:∵等式cos2x-1=3cosx(x∈[0,π]),即2cos2x-2=3cosx,
即2cos2x-3cosx-2=0,求得cosx=2(舍去),或cosx=-$\frac{1}{2}$,∴x=$\frac{2π}{3}$,
故答案为:$\frac{2π}{3}$.
点评 本题主要考查二倍角的余弦公式的应用,根据三角函数的值求角,属于基础题.

练习册系列答案
相关题目
3.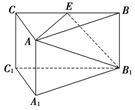 如图,三棱柱ABCA1B1C1中,侧棱AA1垂直底面A1B1C1,底面三角形A1B1C1是正三角形,E是BC中点,则下列叙述正确的是( )
如图,三棱柱ABCA1B1C1中,侧棱AA1垂直底面A1B1C1,底面三角形A1B1C1是正三角形,E是BC中点,则下列叙述正确的是( )
 如图,三棱柱ABCA1B1C1中,侧棱AA1垂直底面A1B1C1,底面三角形A1B1C1是正三角形,E是BC中点,则下列叙述正确的是( )
如图,三棱柱ABCA1B1C1中,侧棱AA1垂直底面A1B1C1,底面三角形A1B1C1是正三角形,E是BC中点,则下列叙述正确的是( )| A. | CC1与B1E是异面直线 | B. | AE与B1C1是异面直线,且AE⊥B1C1 | ||
| C. | AC⊥平面ABB1A1 | D. | A1C1∥平面AB1E |
9.已知等比数列,则“a1>0”是“a2017>0”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
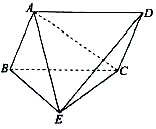 如图四棱锥E-ABCD中,四边形ABCD为平行四边形,△BCE为等边三角形,△ABE是以∠A为直角的等腰直角三角形,且AC=BC.
如图四棱锥E-ABCD中,四边形ABCD为平行四边形,△BCE为等边三角形,△ABE是以∠A为直角的等腰直角三角形,且AC=BC.