题目内容
9.焦点为F1(-2,0),F2(2,0),长轴长为10的椭圆的标准方程为( )| A. | $\frac{x^2}{100}+\frac{y^2}{96}=1$ | B. | $\frac{x^2}{25}+\frac{y^2}{21}=1$ | C. | $\frac{x^2}{96}+\frac{y^2}{100}=1$ | D. | $\frac{x^2}{21}+\frac{y^2}{25}=1$ |
分析 利用已知条件求解a,b,判断椭圆的形状,求解椭圆方程即可.
解答 解:焦点为F1(-2,0),F2(2,0),长轴长为10,
可知焦点在x轴,a=5,c=2,则b=$\sqrt{{a}^{2}-{c}^{2}}$=$\sqrt{21}$.
所求的椭圆方程为:$\frac{x^2}{25}+\frac{y^2}{21}=1$.
故选:B.
点评 本题考查椭圆的简单性质,椭圆方程的求法,考查计算能力.

练习册系列答案
 学期复习一本通学习总动员期末加暑假延边人民出版社系列答案
学期复习一本通学习总动员期末加暑假延边人民出版社系列答案
相关题目
19.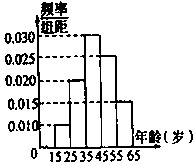 某市电视台为了宣传,举办问答活动,随机对该市15至65岁的人群进行抽样,频率分布直方图及回答问题统计结果如表所示:
某市电视台为了宣传,举办问答活动,随机对该市15至65岁的人群进行抽样,频率分布直方图及回答问题统计结果如表所示:
(1)分别求出a,b,x,y的值;
(2)从第2,3,4组回答正确的人中用分层抽样的方法抽取6人,则第2,3,4组每组应各抽取多少人?
(3)在(2)的前提下,电视台决定在所抽取的6人中随机抽取3人颁发幸运奖,求:所抽取的人中第3组至少有1人获得幸运奖的概率.
 某市电视台为了宣传,举办问答活动,随机对该市15至65岁的人群进行抽样,频率分布直方图及回答问题统计结果如表所示:
某市电视台为了宣传,举办问答活动,随机对该市15至65岁的人群进行抽样,频率分布直方图及回答问题统计结果如表所示:| 组号 | 分组 | 回答正确 的人数 | 回答正确的人数 占本组的概率 |
| 第1组 | [15,25) | 5 | 0.5 |
| 第2组 | [25,35) | a | 0.9 |
| 第3组 | [35,45) | 27 | x |
| 第4组 | [45,55) | b | 0.36 |
| 第5组 | [55,65) | 3 | y |
(2)从第2,3,4组回答正确的人中用分层抽样的方法抽取6人,则第2,3,4组每组应各抽取多少人?
(3)在(2)的前提下,电视台决定在所抽取的6人中随机抽取3人颁发幸运奖,求:所抽取的人中第3组至少有1人获得幸运奖的概率.
17.在正方体ABCD-A1B1C1D1中,CD的中点为M,AA1的中点为N,则异面直线C1M与BN所成角为( )
| A. | 30° | B. | 60° | C. | 90° | D. | 120° |
14.长方体ABCD-A1B1C1D1中,AB=AD=2,AA1=2$\sqrt{2}$,则长方体ABCD-A1B1C1D1的外接球的表面积为( )
| A. | 36π | B. | 28π | C. | 16π | D. | 12π |
 某校收集该校学生从家到学校的时间后,制作成如下的频率分布直方图:
某校收集该校学生从家到学校的时间后,制作成如下的频率分布直方图: