题目内容
14.函数f(x)=ln|1-x|的图象大致形状是( )| A. |  | B. |  | C. |  | D. |  |
分析 化简函数的解析式,然后判断函数的图象即可.
解答 解:函数f(x)=ln|1-x|=$\left\{\begin{array}{l}{ln(x-1),x>1}\\{ln(1-x),x<1}\end{array}\right.$,排除选项A,D,
当x>1时,函数是增函数,排除C.
故选:B.
点评 本题考查函数的图象的判断与应用,是基础题.

练习册系列答案
 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案
相关题目
5.已知t>0,关于x的方程$\sqrt{2}-|x|=\sqrt{t-{x^2}}$,则这个方程的实数的个数是( )
| A. | 0或2 | B. | 0或2或3或4 | C. | 0或2或4 | D. | 0或1或2或3或4 |
2.函数$f(x)=ax-\frac{1}{2}{x^2}-4lnx$在区间[1,+∞)上为减函数,则实数a的取值范围是( )
| A. | (-∞,4) | B. | (-∞,4] | C. | (-∞,5) | D. | (-∞,5] |
9.已知f(x)=sinx+cosx,x∈[0,$\frac{π}{4}$],则y=f(x)值域为( )
| A. | [-$\sqrt{2}$,$\sqrt{2}$] | B. | [1,$\sqrt{2}$] | C. | [-1,$\sqrt{2}$] | D. | [0,$\sqrt{2}$] |
3.某几何体的三视图如图所示,则其体积为( )
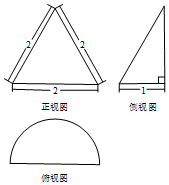

| A. | $\frac{{\sqrt{3}π}}{12}$ | B. | $\frac{π}{6}$ | C. | $\frac{{\sqrt{3}π}}{6}$ | D. | $\frac{{\sqrt{3}π}}{3}$ |
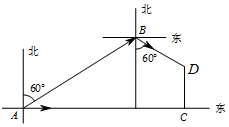 如图,船甲以每小时30公里的速度向正东航行,船甲在A处看到另一船乙在北偏东60°的方向上的B处,且$AB=30\sqrt{3}$公里,正以每小时$5\sqrt{3}$公里的速度向南偏东60°的方向航行,行驶2小时后,甲、乙两船分别到达C、D处,则CD等于$10\sqrt{3}$公里.
如图,船甲以每小时30公里的速度向正东航行,船甲在A处看到另一船乙在北偏东60°的方向上的B处,且$AB=30\sqrt{3}$公里,正以每小时$5\sqrt{3}$公里的速度向南偏东60°的方向航行,行驶2小时后,甲、乙两船分别到达C、D处,则CD等于$10\sqrt{3}$公里.