题目内容
9.函数y=loga(x-3)+2(a>0,a≠1)的图象过定点P,且角α的终边过点P,则的值为sin2α+cos2α( )| A. | $\frac{7}{5}$ | B. | $\frac{6}{5}$ | C. | 4 | D. | 5 |
分析 利用函数的图象经过定点P的坐标,任意角的三角函数的定义,求得sinα和cosα的值,再利用二倍角公式求得要求式子的值.
解答 解:∵函数y=loga(x-3)+2过定点P(4,2),且角α的终边过点P,∴x=4,y=2,r=|OP|=2$\sqrt{5}$,
∴sinα=$\frac{\sqrt{5}}{5}$,cosα=$\frac{2\sqrt{5}}{5}$,∴sin2α+cos2α=2sinαcosα+2cos2α-1=$\frac{7}{5}$,
故选:A.
点评 本题主要考查函数的图象经过定点问题,任意角的三角函数的定义,二倍角公式的应用,属于基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
20.已知0<a1<a2<a3,则使得${({1-{a_i}x})^2}<1({i=1,2,3})$都成立的x的取值范围是( )
| A. | $({0,\frac{1}{a_3}})$ | B. | $({0,\frac{2}{a_3}})$ | C. | $({0,\frac{1}{a_1}})$ | D. | $({0,\frac{2}{a_1}})$ |
17.某几何体的三视图如图所示,则该几何体的体积为( )
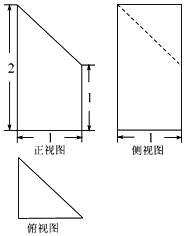

| A. | ${\frac{5}{6}_{\;}}$ | B. | $\frac{2}{3}$ | C. | $\frac{1}{2}$ | D. | $\frac{1}{3}$ |
14.如图所示,一个几何体的三视图中四边形均为边长为4的正方形,则这个几何体的体积为( )


| A. | $64-\frac{32π}{3}$ | B. | 64-16π | C. | $64-\frac{16π}{3}$ | D. | $64-\frac{8π}{3}$ |
19.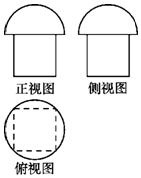 一个几何体的三视图如图所示,其中正视图和侧视图相同,其上部分是半圆,下部分是边长为2的正方形;俯视图是边长为2的正方形及其外接圆.则该几何体的体积为( )
一个几何体的三视图如图所示,其中正视图和侧视图相同,其上部分是半圆,下部分是边长为2的正方形;俯视图是边长为2的正方形及其外接圆.则该几何体的体积为( )
 一个几何体的三视图如图所示,其中正视图和侧视图相同,其上部分是半圆,下部分是边长为2的正方形;俯视图是边长为2的正方形及其外接圆.则该几何体的体积为( )
一个几何体的三视图如图所示,其中正视图和侧视图相同,其上部分是半圆,下部分是边长为2的正方形;俯视图是边长为2的正方形及其外接圆.则该几何体的体积为( )| A. | $4+\frac{2π}{3}$ | B. | $4+\frac{{2\sqrt{2}π}}{3}$ | C. | $8+\frac{{4\sqrt{2}π}}{3}$ | D. | $8+\frac{{8\sqrt{2}π}}{3}$ |