题目内容
14.已知函数f(x)=|x-a|+2|x+b|(a>0,b>0)的最小值为1.(1)求a+b的值;
(2)若$m≤\frac{1}{a}+\frac{2}{b}$恒成立,求实数m的最大值.
分析 (1)写出分段函数,得出f(x)min=a+b,即可求a+b的值;
(2)因为a>0,b>0,且a+b=1,利用“1”的代换,求最值,根据$m≤\frac{1}{a}+\frac{2}{b}$恒成立,求实数m的最大值.
解答 解:(1)$f(x)=\left\{\begin{array}{l}-3x+a-2b,x≤-b\\ x+a+2b,-b<x<a\\ 3x-a+2b,x≥a.\end{array}\right.$
f(x)在区间(-∞,-b]上递减,在区间[-b,+∞)上递增,
所以f(x)min=a+b.
所以a+b=1.
(2)因为a>0,b>0,且a+b=1,
所以$\frac{1}{a}+\frac{2}{b}=({a+b})({\frac{1}{a}+\frac{2}{b}})=3+\frac{b}{a}+\frac{2a}{b}$,
又因为$3+\frac{b}{a}+\frac{2a}{b}≥3+2\sqrt{\frac{b}{a}•\frac{2a}{b}}$,当且仅当$\frac{b}{a}=\frac{2a}{b}$时,等号成立,
所以$a=\sqrt{2}-1,b=2-\sqrt{2}$时,$\frac{1}{a}+\frac{2}{b}$有最小值$3+2\sqrt{2}$.
所以$m≤3+2\sqrt{2}$,所以实数m的最大值为$3+2\sqrt{2}$.
点评 本题考查绝对值函数,考查基本不等式的运用,正确转化是关键.

练习册系列答案
 学而优衔接教材南京大学出版社系列答案
学而优衔接教材南京大学出版社系列答案 小学课堂作业系列答案
小学课堂作业系列答案
相关题目
2.已知全集U=R,集合M={x||x|<1},N={y|y=2x,x∈R},则集合∁U(M∪N)等于( )
| A. | (-∞,-1] | B. | (-1,2) | C. | (-∞,-1]∪[2,+∞) | D. | [2,+∞) |
19.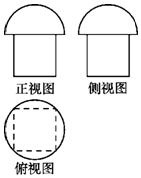 一个几何体的三视图如图所示,其中正视图和侧视图相同,其上部分是半圆,下部分是边长为2的正方形;俯视图是边长为2的正方形及其外接圆.则该几何体的体积为( )
一个几何体的三视图如图所示,其中正视图和侧视图相同,其上部分是半圆,下部分是边长为2的正方形;俯视图是边长为2的正方形及其外接圆.则该几何体的体积为( )
 一个几何体的三视图如图所示,其中正视图和侧视图相同,其上部分是半圆,下部分是边长为2的正方形;俯视图是边长为2的正方形及其外接圆.则该几何体的体积为( )
一个几何体的三视图如图所示,其中正视图和侧视图相同,其上部分是半圆,下部分是边长为2的正方形;俯视图是边长为2的正方形及其外接圆.则该几何体的体积为( )| A. | $4+\frac{2π}{3}$ | B. | $4+\frac{{2\sqrt{2}π}}{3}$ | C. | $8+\frac{{4\sqrt{2}π}}{3}$ | D. | $8+\frac{{8\sqrt{2}π}}{3}$ |
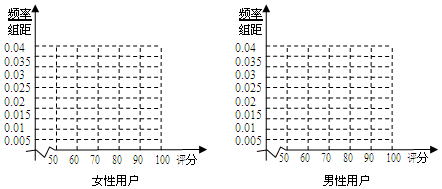
3.某手机厂商推出一款6寸大屏手机,现对500名该手机用户(200名女性,300名男性)进行调查,对手机进行评分,评分的频数分布表如下:
(1)完成下列频率分布直方图,并指出女性用户和男性用户哪组评分更稳定(不计算具体值,给出结论即可);
(2)根据评分的不同,运用分层抽样从男性用户中抽取20名用户,在这20名用户中,从评分不低于80分的用户中任意抽取3名用户,求3名用户中评分小于90分的人数的分布列和期望.
| 女性用户 | 分值区间 | [50,60) | [60,70) | [70,80) | [80,90) | [90,100] |
| 频数 | 20 | 40 | 80 | 50 | 10 | |
| 男性用户 | 分值区间 | [50,60) | [60,70) | [70,80) | [80,90) | [90,100] |
| 频数 | 45 | 75 | 90 | 60 | 30 |

(2)根据评分的不同,运用分层抽样从男性用户中抽取20名用户,在这20名用户中,从评分不低于80分的用户中任意抽取3名用户,求3名用户中评分小于90分的人数的分布列和期望.