题目内容
用反证法证明命题：“若实系数一元二次方程ax2+bx+c=0（a≠0）有实数根，那么b2-4ac≥0”时，下列假设正确的是（ ）
| A、假设b2-4ac≤0 |
| B、假设b2-4ac＜0 |
| C、假设b2-4ac≥0 |
| D、假设b2-4ac＞0 |
考点：反证法与放缩法
专题：证明题,反证法
分析：用反证法证明数学命题时，应先假设命题的否定成立，求得命题的否定，即可得到结论．
解答：
解：由于用反证法证明数学命题时，应先把要证的结论进行否定，得到要证的结论的反面．
而命题：“若实系数一元二次方程ax2+bx+c=0（a≠0）有实数根，那么b2-4ac≥0”的否定为：“b2-4ac＜0”，
故选：B．
而命题：“若实系数一元二次方程ax2+bx+c=0（a≠0）有实数根，那么b2-4ac≥0”的否定为：“b2-4ac＜0”，
故选：B．
点评：本题考查用反证法证明命题的方法，求出命题的否定，是解题的关键．
练习册系列答案
相关题目
六个同学平均分到甲乙两个班中，分配的种数是（ ）
| A、20 | B、40 | C、60 | D、80 |
下列四个条件中，能确定一个平面的是（ ）
| A、一条直线和一个点 |
| B、空间两条直线 |
| C、空间任意三点 |
| D、两条平行直线 |
互相平行的三条直线，最多可以确定的平面个数为（ ）
| A、1个 | B、2个 | C、3个 | D、4个 |
已知函数f（x）在x0处可导，则
等于（ ）
| lim |
| △x→0 |
| f(x0-2h)-f(x0) |
| h |
| A、2f′（x0） |
| B、-f′（-x0） |
| C、-f′（x0） |
| D、-2f′（x0） |
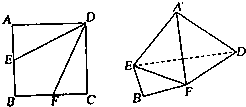如图，在边长为2的正方形ABCD中，E，F分别是AB，BC的中点，将△ADE，△CDF分别沿DE，DF折起，使A，C两点重合于点A′．