题目内容
8.已知sinα-sinβ=1-$\frac{\sqrt{3}}{2}$,cosα-cosβ=$\frac{1}{2}$,则cos(α-β)=( )| A. | -$\frac{\sqrt{3}}{2}$ | B. | -$\frac{1}{2}$ | C. | $\frac{1}{2}$ | D. | $\frac{\sqrt{3}}{2}$ |
分析 对已知条件sinα-sinβ=1-$\frac{\sqrt{3}}{2}$,cosα-cosβ=$\frac{1}{2}$,两边平方再相加即可得到答案.
解答 解:∵sinα-sinβ=1-$\frac{\sqrt{3}}{2}$,cosα-cosβ=$\frac{1}{2}$,
∴(cosα-cosβ)2=$\frac{1}{4}$,(sinα-sinβ)2=$\frac{7}{4}$-$\sqrt{3}$.
两式相加,得2-2cos(α-β)=2-$\sqrt{3}$.
∴cos(α-β)=$\frac{\sqrt{3}}{2}$.
故选:D.
点评 本题主要考查两角和与差的余弦公式在三角函数化简求值中的应用,考查了计算能力和转化思想,属于基础题.

练习册系列答案
 初中暑期衔接系列答案
初中暑期衔接系列答案
相关题目
18.若集合A={x|x<3},B={x|x>0},则A∪B=( )
| A. | {x|0<x<3} | B. | {x|x>0} | C. | {x|x<3} | D. | R |
3.如图,在网格中粗线显示的为某几何体的三视图(正方形网格的边长为1),则该几何体的体积为( )
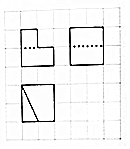

| A. | 5 | B. | 6 | C. | 6.5 | D. | 7 |
13.若实数x,y满足$\left\{\begin{array}{l}x-y+1≥0\\ x+y≥0\\ x≤0\end{array}\right.$,则z=x-2y的最小值是( )
| A. | 0 | B. | $\frac{3}{2}$ | C. | -2 | D. | $-\frac{3}{2}$ |
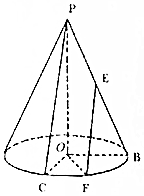 已知圆锥的高PO=4,底面半径OB=2,E为母线PB的中点,C为底面圆周上一点,满足OB⊥OC,F为弧BC上一点,且∠BOF=$\frac{π}{3}$.
已知圆锥的高PO=4,底面半径OB=2,E为母线PB的中点,C为底面圆周上一点,满足OB⊥OC,F为弧BC上一点,且∠BOF=$\frac{π}{3}$.