题目内容
1.若直线l:(a2-1)x-y-2a+1=0不过第二象限,则a的取值范围为( )| A. | (-∞,$\frac{1}{2}$] | B. | [$\frac{1}{2}$,+∞) | C. | (-∞,1] | D. | [1,+∞) |
分析 将直线一般式方程化为斜截式,根据直线的特征列出不等式组,求出a的取值范围.
解答 解:由(a2-1)x-y-2a+1=0得,
直线l的方程:y=(a2-1)x-2a+1,
∵直线l不过第二象限,
∴$\left\{\begin{array}{l}{{a}^{2}-1≥0}\\{-2a+1≤0}\end{array}\right.$,解得a≥1,
∴a的取值范围为[1,+∞),
故选:D.
点评 本题考查直线一般式方程,以及直线的特征的应用,属于基础题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
11.直线x-y+1=0的倾斜角为( )
| A. | 90° | B. | 45° | C. | 135° | D. | 60° |
12.抛物线y=$\frac{1}{8}$x2的焦点坐标为( )
| A. | ($\frac{1}{32}$,0) | B. | (0,$\frac{1}{32}$) | C. | (0,4) | D. | (0,2) |
9.已知一组样本数据(xi,yi)如表
设其线性回归方程$\widehat{y}$=bx+a,若已求出b=0.7,则线性回归方程为( )
| x | 3 | 4 | 5 | 6 |
| y | 2.5 | 3 | 4 | 4.5 |
| A. | $\widehat{y}$=0.7x+0.35 | B. | $\widehat{y}$=0.7x+4.5 | C. | $\widehat{y}$=0.7x-0.35 | D. | $\widehat{y}$=0.7x-4.5 |
13.若实数x,y满足$\left\{\begin{array}{l}x-y+1≥0\\ x+y≥0\\ x≤0\end{array}\right.$,则z=x-2y的最小值是( )
| A. | 0 | B. | $\frac{3}{2}$ | C. | -2 | D. | $-\frac{3}{2}$ |
11.已知集合A={x|y=log2x,y∈Z},B={1,2,3,4,5,6,7,8,9},则A∩B=( )
| A. | {1,2,3,4} | B. | {2,4,6,8} | C. | {1,2,4,8} | D. | {2,4,8} |
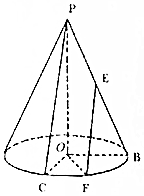 已知圆锥的高PO=4,底面半径OB=2,E为母线PB的中点,C为底面圆周上一点,满足OB⊥OC,F为弧BC上一点,且∠BOF=$\frac{π}{3}$.
已知圆锥的高PO=4,底面半径OB=2,E为母线PB的中点,C为底面圆周上一点,满足OB⊥OC,F为弧BC上一点,且∠BOF=$\frac{π}{3}$.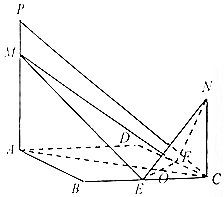 如图,已知E,F分别是正方形ABCD边BC、CD的中点,EF与AC交于点O,PA,NC都垂直于平面ABCD,且PA=AB=4,NC=2,M是线段PA上的一动点.
如图,已知E,F分别是正方形ABCD边BC、CD的中点,EF与AC交于点O,PA,NC都垂直于平面ABCD,且PA=AB=4,NC=2,M是线段PA上的一动点.