题目内容
已知,函数f(x)=
.
(1)如果x≥0时,f(x)≤
恒成立,求m的取值范围;
(2)当a≤2时,求证:f(x)ln(2x+a)<x+1.
| x+1 |
| e2x |
(1)如果x≥0时,f(x)≤
| m |
| x+1 |
(2)当a≤2时,求证:f(x)ln(2x+a)<x+1.
考点:导数在最大值、最小值问题中的应用
专题:导数的综合应用
分析:(1)根据条件化简f(x)≤
得m≥
>0,转化为
≥
,令g(x)=
(x≥0)利用导数求出其最大值,即可确定m的取值范围;
(2)利用分析法,要证f(x)ln(2x+a)<x+1可转化为证
ln(2x+a)<x+1,由a≤2得只需证h(t)=et-ln(t+2)>0,(t=2x>-2)即可,利用导数求出h(t)的最小值大于0即可得证.
| m |
| x+1 |
| (x+1)2 |
| e2x |
| m |
| x+1 |
| ex |
| x+1 |
| ex |
(2)利用分析法,要证f(x)ln(2x+a)<x+1可转化为证
| x+1 |
| e2x |
解答:
解:(1)∵x≥0,f(x)≤
,
∴m≥
>0,
∴
≥
.
令g(x)=
(x≥0),
∵g′(x)=
≤0,
∴g(x)递减,
∴g(x)max=g(0)=1,
∴m的取值范围是[1,+∞)
(2)证明:当a≤2时,
p(x)=f(x)ln(2x+a)-(x+1)的定义域(-
,+∞)⊆(-1,+∞),
∴x+1>0,
要证
ln(2x+a)<x+1,
只需证ln(2x+a)<e2x,
又∵a≤2,
∴只需证ln(2x+2)<e2x,
即证h(t)=et-ln(t+2)>0,(t=2x>-2)
∵h′(x)=et-
(t>2)递增,
h′(-1)=
-1<0,h′(0)=1-
>0,
∴必有t0∈(-1,0),使h′(t0)=0,
即et0=
,
即t0=-ln(t0+2),
且在(-2,t0)上,h′(t)<0;
在(t0,+∞)上,h′(t)>0,
∴h(t)min=et0-ln(t+2)
=
+t0
=
>0,
∴h(t)=et-ln(t+2)>0,
即f(x)ln(2x+a)<x+1.
| m |
| x+1 |
∴m≥
| (x+1)2 |
| e2x |
∴
| m |
| x+1 |
| ex |
令g(x)=
| x+1 |
| ex |
∵g′(x)=
| -x |
| ex |
∴g(x)递减,
∴g(x)max=g(0)=1,
∴m的取值范围是[1,+∞)
(2)证明:当a≤2时,
p(x)=f(x)ln(2x+a)-(x+1)的定义域(-
| a |
| 2 |
∴x+1>0,
要证
| x+1 |
| e2x |
只需证ln(2x+a)<e2x,
又∵a≤2,
∴只需证ln(2x+2)<e2x,
即证h(t)=et-ln(t+2)>0,(t=2x>-2)
∵h′(x)=et-
| 1 |
| t+2 |
h′(-1)=
| 1 |
| e |
| 1 |
| 2 |
∴必有t0∈(-1,0),使h′(t0)=0,
即et0=
| 1 |
| t0+2 |
即t0=-ln(t0+2),
且在(-2,t0)上,h′(t)<0;
在(t0,+∞)上,h′(t)>0,
∴h(t)min=et0-ln(t+2)
=
| 1 |
| t0+2 |
=
| (t0+1)2 |
| t0+2 |
∴h(t)=et-ln(t+2)>0,
即f(x)ln(2x+a)<x+1.
点评:本题考查导数在研究函数单调性和最值中的应用,属于难题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
已知集合A={x|x2-2x<0},B={x|x≤-1或x>1},则A∩(∁RB)=( )
| A、{x|0<x<1} |
| B、{x|1≤x<2} |
| C、{x|0<x≤1} |
| D、{x|1<x<2} |
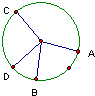 如图,转盘被分成了4部分,其中∠AOB=∠COD=90°,则随意转动转盘,指针指向∠AOB和∠COD所在区域的概率是
如图,转盘被分成了4部分,其中∠AOB=∠COD=90°,则随意转动转盘,指针指向∠AOB和∠COD所在区域的概率是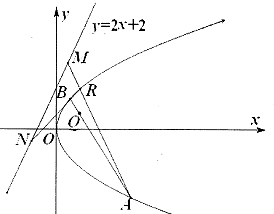 已知抛物线C的方程为y2=2px(p>0),点R(1,2)在抛物线C上.
已知抛物线C的方程为y2=2px(p>0),点R(1,2)在抛物线C上.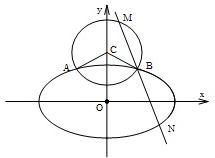 已知离心率为
已知离心率为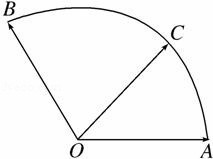 给定两个平面向量
给定两个平面向量