题目内容
在△ABC中，AB=2
，AC=3，sinC=2sinA．
（Ⅰ）求△ABC的面积S；
（Ⅱ）求cos（2A+
）的值．
| 5 |
（Ⅰ）求△ABC的面积S；
（Ⅱ）求cos（2A+
| 2π |
| 3 |
考点：余弦定理,正弦定理
专题：三角函数的求值
分析：（Ⅰ）由AB，AC，以及sinC=2sinA，利用正弦定理求出BC的长，再利用余弦定理表示出cosA，将三边上代入求出cosA的值，进而确定出sinA的值，由AB，AC，以及sinnA的值，利用三角形面积公式即可求出△ABC的面积S；
（Ⅱ）由sinA与cosA的值，利用二倍角的正弦、余弦函数公式求出sin2A与cos2A的值，原式利用两角和与差的余弦函数公式化简，将各自的值代入计算即可求出值．
（Ⅱ）由sinA与cosA的值，利用二倍角的正弦、余弦函数公式求出sin2A与cos2A的值，原式利用两角和与差的余弦函数公式化简，将各自的值代入计算即可求出值．
解答：
解：（Ⅰ）在△ABC中，AB=2
，AC=3，sinC=2sinA，
∴根据正弦定理：
=
，得BC=
=
AB=
，
根据余弦定理得：cosA=
=
，
∵A∈（0，π），∴sinA=
=
，
则S=
AB•AC•sinA=
×2
×3×
=3；
（Ⅱ）∵sinA=
，cosA=
，
∴sin2A=2sinAcosA=
，cos2A=cos2A-sin2A=
，
∴cos（2A+
）=cos2Acos
-sin2Asin
=
×（-
）-
×
=
．
| 5 |
∴根据正弦定理：
| AB |
| sinC |
| BC |
| sinA |
| ABsinA |
| sinC |
| 1 |
| 2 |
| 5 |
根据余弦定理得：cosA=
| AB2+AC2-BC2 |
| 2AB•AC |
2
| ||
| 5 |
∵A∈（0，π），∴sinA=
| 1-cos2A |
| ||
| 5 |
则S=
| 1 |
| 2 |
| 1 |
| 2 |
| 5 |
| ||
| 5 |
（Ⅱ）∵sinA=
| ||
| 5 |
2
| ||
| 5 |
∴sin2A=2sinAcosA=
| 4 |
| 5 |
| 3 |
| 5 |
∴cos（2A+
| 2π |
| 3 |
| 2π |
| 3 |
| 2π |
| 3 |
| 3 |
| 5 |
| 1 |
| 2 |
| 4 |
| 5 |
| ||
| 2 |
-3-4
| ||
| 10 |
点评：此题考查了正弦、余弦定理，两角和与差的余弦函数公式，以及三角形面积公式，熟练掌握公式及定理是解本题的关键．
练习册系列答案
时刻准备着暑假作业原子能出版社系列答案
相关题目
设集合A={x∈R|-1≤x≤1}，B={x∈R|x（x-3）≤0}，则A∩B等于（ ）
| A、{x∈R|-1≤x≤3} |
| B、{x∈R|0≤x≤3} |
| C、{x∈R|-1≤x≤0} |
| D、{x∈R|0≤x≤1} |
在[-1，2]上随机取一个实数，则|x-1|≤1的概率是（ ）
A、
| ||
B、
| ||
C、
| ||
D、
|
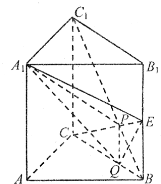如图在直三棱柱ABC-A1B1C1中，∠BAC=90°，AB=