题目内容
知圆C方程:x2+y2-8x+15=0,直线l方程:y=kx-2
①若l与圆相切,求K的值;
②若l上至少存在一点,使得以该点为圆心,1为半径的圆与圆C有公共点,求K的取值范围.
①若l与圆相切,求K的值;
②若l上至少存在一点,使得以该点为圆心,1为半径的圆与圆C有公共点,求K的取值范围.
考点:直线和圆的方程的应用
专题:直线与圆
分析:①根据直线与圆相切得出:
=1,
②根据题意得出可知圆心O(4,0),到直线y=kx-2的距离d≤2,即
≤2,求解即可.
| |4k-2| | ||
|
②根据题意得出可知圆心O(4,0),到直线y=kx-2的距离d≤2,即
| |4k-2| | ||
|
解答:
解:①∵圆C方程:x2+y2-8x+15=0,
∴圆心O(4,0),半径r=1,
∵直线l方程:y=kx-2,若l与圆相切,
∴
=1,
即k=
或k=
,
②∵若l上至少存在一点,使得以该点为圆心,1为半径的圆与圆C有公共点,
∴可知圆心O(4,0),到直线y=kx-2的距离d≤2,
即
≤2,
解得:0≤k≤
,
故k的取值范围:0≤k≤
,
∴圆心O(4,0),半径r=1,
∵直线l方程:y=kx-2,若l与圆相切,
∴
| |4k-2| | ||
|
即k=
8+
| ||
| 15 |
8-
| ||
| 15 |
②∵若l上至少存在一点,使得以该点为圆心,1为半径的圆与圆C有公共点,
∴可知圆心O(4,0),到直线y=kx-2的距离d≤2,
即
| |4k-2| | ||
|
解得:0≤k≤
| 4 |
| 3 |
故k的取值范围:0≤k≤
| 4 |
| 3 |
点评:本题综合考察了直线与圆.圆与圆的位置关系,结合不等式求解问题,属于中档题,关键是列出不等式.

练习册系列答案
相关题目
若函数f(x)=(a2-2a-3)x2+(a-3)x+1的定义域和值域都为R,则( )
| A、a=-1或a=3 | B、a=-1 |
| C、a=3 | D、a不存在 |
在△ABC中,角A、B、C所对的边分别为a,b,c,若
•
=
•
=1,那么c等于( )
| AB |
| AC |
| BA |
| BC |
| A、2 | ||
B、
| ||
C、
| ||
| D、4 |
设集合M={a,a+1},N={x∈R|x2≤4},若M∪N=N,则实数a的取值范围为( )
| A、[-1,2] |
| B、[-2,1] |
| C、[-2,2] |
| D、(-∞,-2]∪[2,+∞) |
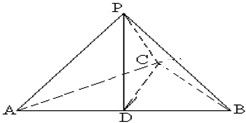 如图,已知三棱锥P-ABC,D为AB的中点,且△PDB是正三角形,PA⊥PC.求证:PC⊥BC.
如图,已知三棱锥P-ABC,D为AB的中点,且△PDB是正三角形,PA⊥PC.求证:PC⊥BC.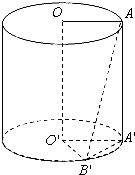 圆柱的高为4cm,底面半径为3cm,上底面一条半径OA与下底面一条半径O′B′成60°角,求:
圆柱的高为4cm,底面半径为3cm,上底面一条半径OA与下底面一条半径O′B′成60°角,求: