题目内容
在△ABC中，角A、B、C所对的边分别为a，b，c，若
•
=
•
=1，那么c等于（ ）
| AB |
| AC |
| BA |
| BC |
| A、2 | ||
B、
| ||
C、
| ||
| D、4 |
考点：平面向量数量积的运算
专题：平面向量及应用
分析：由
•
=
•
=1，转化为一个三角方程，解方程即可证明：A=B，再结合余弦定理，可构造一个关于c的方程，解方程易求c值．
| AB |
| AC |
| BA |
| BC |
解答：
解：∵
•
=
•
=1，
∴bccosA=accosB，即bcosA=acosB
由正弦定理得sinBcosA=sinAcosB
∴sin（A-B）=0
∵-π＜A-B＜π
∴A-B=0，∴A=B
∵
•
=1，∴bccosA=1
由余弦定理得bc•
=1，即b2+c2-a2=2
∵由A=B
得a=b，∴c2=2，∴c=
；
故选B．
| AB |
| AC |
| BA |
| BC |
∴bccosA=accosB，即bcosA=acosB
由正弦定理得sinBcosA=sinAcosB
∴sin（A-B）=0
∵-π＜A-B＜π
∴A-B=0，∴A=B
∵
| AB |
| AC |
由余弦定理得bc•
| b2+c2-a2 |
| 2bc |
∵由A=B
得a=b，∴c2=2，∴c=
| 2 |
故选B．
点评：本题考查了向量数量积以及正弦定理和余弦定理的运用，在判断三角形形状时，要注意对角的范围进行分析，即求角的大小需要两个条件：该角的一个三角函数值和该角的范围，缺一不可，正、余弦定理是解三解形必用的数学工具．
练习册系列答案
阳光课堂课时优化作业系列答案
相关题目
已知正四棱锥V-ABCD可绕着AB任意旋转，CD∥平面α．若AB=2，VA=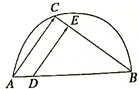
如图，半圆的直径AB=6，C是半圆上的一点，D、E分别是AB、BC上的点，且AD=1，BE=4，DE=3．