题目内容
设集合M={a,a+1},N={x∈R|x2≤4},若M∪N=N,则实数a的取值范围为( )
| A、[-1,2] |
| B、[-2,1] |
| C、[-2,2] |
| D、(-∞,-2]∪[2,+∞) |
考点:一元二次不等式的解法,并集及其运算
专题:集合
分析:解一元二次不等式化简集合N,再结合M∪N=N列不等式组即可求出实数a的取值范围.
解答:
解:由N={x∈R|x2≤4}={x∈R|-2≤x≤2},又M∪N=N,
则
,解得:-2≤a≤1.
∴实数a的取值范围为-2≤a≤1.
故选:B.
则
|
∴实数a的取值范围为-2≤a≤1.
故选:B.
点评:本题考查了并集及其运算,考查了一元二次不等式的解法,是基础题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
已知b为如图所示的程序框图输出的结果,则二项式(
-
)6的展开式中的常数项是( )

| bx |
| 1 | ||
|

| A、-20 | B、20 |
| C、-540 | D、540 |
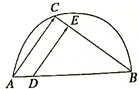 如图,半圆的直径AB=6,C是半圆上的一点,D、E分别是AB、BC上的点,且AD=1,BE=4,DE=3.
如图,半圆的直径AB=6,C是半圆上的一点,D、E分别是AB、BC上的点,且AD=1,BE=4,DE=3.