题目内容
已知函数f(x)=2cos2x-sin(2x-
).
(1)求函数f(x)的单调递增区间;
(2)当x∈[-
,
]时,求f(x)的最大值和最小值.
| 7π |
| 6 |
(1)求函数f(x)的单调递增区间;
(2)当x∈[-
| π |
| 6 |
| π |
| 3 |
考点:两角和与差的正弦函数,二倍角的余弦,正弦函数的单调性,三角函数的最值
专题:计算题,三角函数的求值,三角函数的图像与性质
分析:(1)化简可得f(x)=1+sin(2x+
).令2kπ-
≤2x+
≤2kπ+
,k∈Z可解得kπ-
≤x≤kπ+
,k∈Z
(2)由x∈[-
,
],解得-
≤2x+
≤
,由正弦函数的单调性知f(x)max=2,f(x)min=f(-
)=1-
=
.
| π |
| 6 |
| π |
| 2 |
| π |
| 6 |
| π |
| 2 |
| π |
| 3 |
| π |
| 6 |
(2)由x∈[-
| π |
| 6 |
| π |
| 3 |
| π |
| 6 |
| π |
| 6 |
| 5π |
| 6 |
| π |
| 6 |
| 1 |
| 2 |
| 1 |
| 2 |
解答:
解:(1)f(x)=2cos2x-sin(2x-
)=1+cos2x+sin(2x-
)=1+sin(2x+
).
令2kπ-
≤2x+
≤2kπ+
,k∈Z可解得kπ-
≤x≤kπ+
,k∈Z
故函数f(x)的单调递增区间为:[kπ-
,kπ+
],k∈Z.
(2)∵x∈[-
,
]∴解得-
≤2x+
≤
∴由正弦函数的单调性知f(x)max=2,f(x)min=f(-
)=1-
=
.
| 7π |
| 6 |
| π |
| 6 |
| π |
| 6 |
令2kπ-
| π |
| 2 |
| π |
| 6 |
| π |
| 2 |
| π |
| 3 |
| π |
| 6 |
故函数f(x)的单调递增区间为:[kπ-
| π |
| 3 |
| π |
| 6 |
(2)∵x∈[-
| π |
| 6 |
| π |
| 3 |
| π |
| 6 |
| π |
| 6 |
| 5π |
| 6 |
∴由正弦函数的单调性知f(x)max=2,f(x)min=f(-
| π |
| 6 |
| 1 |
| 2 |
| 1 |
| 2 |
点评:本题主要考查了正弦函数的单调性,三角函数的最值,两角和与差的正弦函数,属于基本知识的考查.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
在正项等比数列{an}中3a1,
a3,2a2成等差数列,则
等于( )
| 1 |
| 2 |
| a2013+a2014 |
| a2011+a2012 |
| A、3或-1 | B、9或1 | C、1 | D、9 |
已知f(x)=sin(ωx+
),(ω>0)的图象与y=1的图象的两相邻交点间的距离为π,
要得到y=f(x)的图象,只须把y=sinωx的图象( )
| π |
| 3 |
要得到y=f(x)的图象,只须把y=sinωx的图象( )
A、向左平移
| ||
B、向右平移
| ||
C、向左平移
| ||
D、向右平移
|
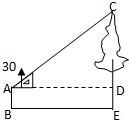 如图,小明利用有一个锐角是30°的三角板测量一棵树的高度,已知他与树之间的水平距离BE为5m,AB为1.5m(即小明的眼睛距地面的距离),那么这棵树高是( )
如图,小明利用有一个锐角是30°的三角板测量一棵树的高度,已知他与树之间的水平距离BE为5m,AB为1.5m(即小明的眼睛距地面的距离),那么这棵树高是( )A、(
| ||||||
B、(5
| ||||||
C、
| ||||||
| D、4m |
已知向量
,
的夹角为120°,|
|=2,且
•
=-8,则|
|=( )
| a |
| b |
| a |
| a |
| b |
| b |
| A、6 | B、7 | C、8 | D、9 |
将函数y=cos(
-2x)的图象向右平移
个单位后所得的图象的一个对称轴是( )
| π |
| 6 |
| π |
| 12 |
A、x=
| ||
B、x=
| ||
C、x=
| ||
D、x=
|